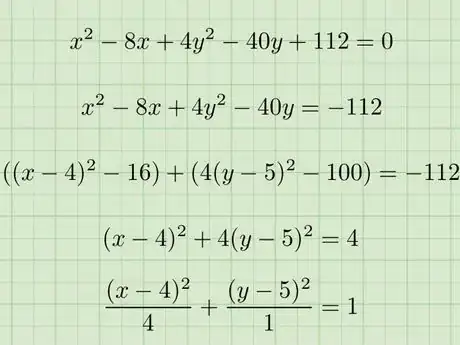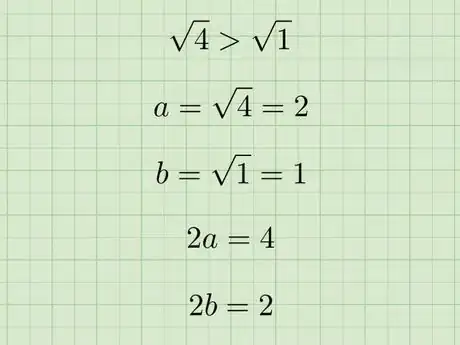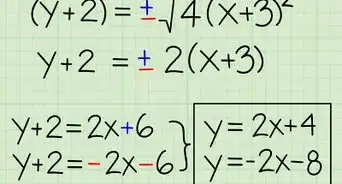How to Graph an Ellipse

Last Updated: December 24, 2021 References

An ellipse is one type of conic section (you can think of a conic section as the shape formed by slicing through a cone) that looks like an oval. More formally, it is defined as the curve formed by all the points such that the sum of its distances from each of the two foci (two specific points) is constant.^{[1]
X
Research source} Graphing an ellipse may seem intimidating at first, but it's easier than you think! This wikiHow will provide a step-by-step guide on graphing an ellipse.

Part 1

Part 1 of 2:

Understanding the Properties of Ellipses^{[2]
X
Research source}^{[3]
X
Research source}

1
Know what an ellipse is.^{[4]
X
Research source} An ellipse is the curve formed by all the points such that the sum of its distances from each of the two foci (two specific points) is constant.^{[5]
X
Research source}
- Intuitively, it's a squashed circle, and it takes the shape of an oval.
- The ellipse is also one of the shapes you can get by slicing a cone (these shapes are called conic sections).
Fun Fact: The ellipse pops up in many real-life situations. For example, the Earth's orbit around the Sun and the Moon's orbit around Earth are both in the shape of an ellipse.^{[6]
X
Trustworthy Source
NASA
Independent agency of the U.S. government in charge of the aerospace research and the space program
Go to source}
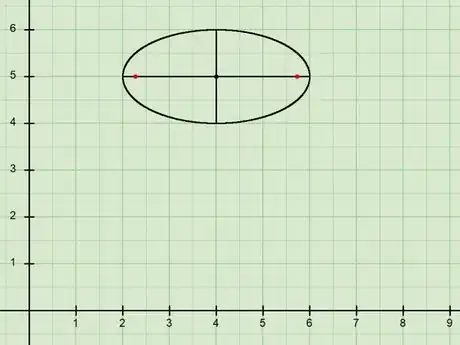
2
Know about the two foci of the ellipse. The foci (plural for "focus") are two points inside the ellipse. Since an ellipse is the curve formed by all the points such that the sum of its distances from each of the two foci is constant, the foci are one of the main defining inputs for an ellipse, along with the constant distance sum.^{[7]
X
Research source}
- When both foci are at the same place, the ellipse is a circle.^{[8]
  X
  Research source}
Fun Fact: Rays (lines going in one direction) from one focus are reflected to the other focus. This is seen in whispering galleries, where a whisper from one focus of an ellipsoid can be heard at the other focus, but can't be heard anywhere else.^{[9]
X
Research source} A famous example of a whispering gallery is the Grand Central Terminal.^{[10]
X
Research source}

Advertisement
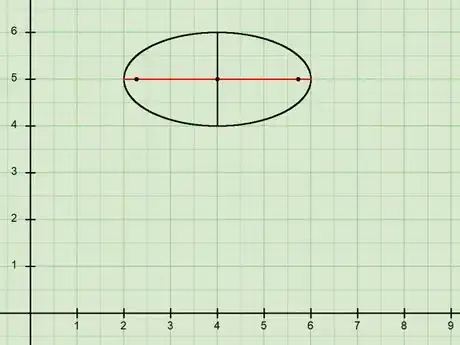
3
Note the major axis. The major axis is the chord that passes through both foci. Note that a chord of an ellipse is a line segment with endpoints on the ellipse.
- You can also think of the major axis as the longest possible chord.
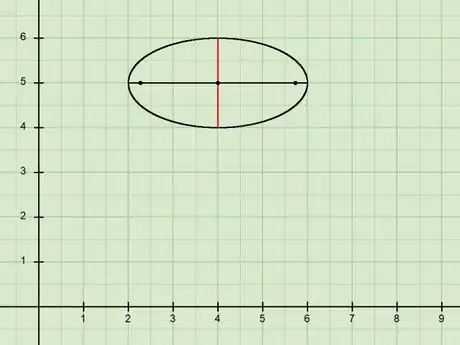
4
Note the minor axis. The minor axis is the chord that is perpendicular to (forms a right angle with) and bisects the major axis.
- The minor axis is also the shortest possible diameter of an ellipse (a diameter is a chord that passes through the center, going from one side of the ellipse to the other).^{[11]
  X
  Research source}
5
Know what the center of an ellipse is. The center of an ellipse is defined as the midpoint of the two foci.
- Alternatively, it is also where the major and minor axes intersect.
- It can also be defined as the midpoint of the major and minor axes.
- Intuitively, it's the "middle" of the ellipse.

Part 2

Part 2 of 2:

Graphing the Ellipse^{[12]
X
Research source}

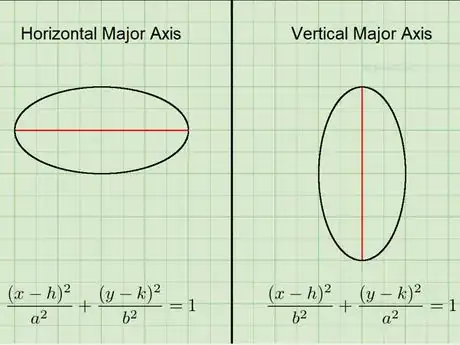
1
Know the form for an ellipse.^{[13]
X
Research source} If the major axis is parallel to the x-axis (i.e., it is horizontal), the form for an ellipse is ${\frac {(x-h)^{2}}{a^{2}}}+{\frac {(y-k)^{2}}{b^{2}}}=1$ $\frac{(x-h)^2}{a^2}+\frac{(y-k)^2}{b^2}=1$ , where $a>b>0$ $a>b>0$ . If the major axis is parallel to the y-axis (i.e., it is vertical), the form for an ellipse is ${\frac {(x-h)^{2}}{b^{2}}}+{\frac {(y-k)^{2}}{a^{2}}}=1$ $\frac{(x-h)^2}{b^2}+\frac{(y-k)^2}{a^2}=1$ , again where $a>b>0$ $a>b>0$ .
- It's possible for $a$ to be equal to $b$ . In that case, the ellipse would be a circle, which is easier to graph.
Fun Fact: An ellipse rotated by an angle $\alpha$ counterclockwise is of the form ${\frac {((x-h)\cos \alpha +(y-k)\sin \alpha )^{2}}{a^{2}}}+{\frac {((x-h)\sin \alpha -(y-k)\cos \alpha )^{2}}{b^{2}}}=1$ , where $a>b>0$ , though this is more advanced and doesn't appear too often.^{[14]
X
Research source}^{[15]
X
Research source} You can also check that this is consistent with our forms above when $\alpha =0^{\circ }$ and $\alpha =90^{\circ }$ .
2
Modify the equation you're given to match the form for an ellipse. If you're given an equation such as $x^{2}-8x+4y^{2}-40y+112=0$ $x^{2}-8x+4y^{2}-40y+112=0$ , you'll need to modify the equation by completing the square before continuing.
- Move all constants to the right side. In our example, the equation would become $x^{2}-8x+4y^{2}-40y=-112$ .
- Complete the square. Our equation would become $((x-4)^{2}-16)+(4(y-5)^{2}-100)=-112$ .
- Move all constants to the right side again. Our equation would become $(x-4)^{2}+4(y-5)^{2}=4$ .
- Divide both sides by the constant on the right side. We would get ${\frac {(x-4)^{2}}{4}}+{\frac {(y-5)^{2}}{1}}=1$ .
3
Find the center of the ellipse. In both forms for an ellipse, the center of the ellipse is $(h,k)$ $(h,k)$ .
- For example, the center of the ellipse ${\frac {(x-4)^{2}}{4}}+{\frac {(y-5)^{2}}{1}}=1$ would be $(4,5)$ .
- Be careful with the negative sign – the center of the ellipse ${\frac {(x+4)^{2}}{4}}+{\frac {(y+5)^{2}}{1}}=1$ would be $(-4,-5)$ , and not $(4,5)$ .
- Also, remember that $h$ and/or $k$ could be zero.
4
Find the length of the major and minor axes. The length of the major axis is $2a$ $2a$ and the length of the minor axis is $2b$ $2b$ . Remember that that $a>b>0$ $a>b>0$ .
- In our example, since ${\sqrt {4}}>{\sqrt {1}}$ , we have that $a={\sqrt {4}}=2$ and $b={\sqrt {1}}=1$ . So, the length of the major axis is $2a=4$ and the length of the minor axis is $2b=2$ .
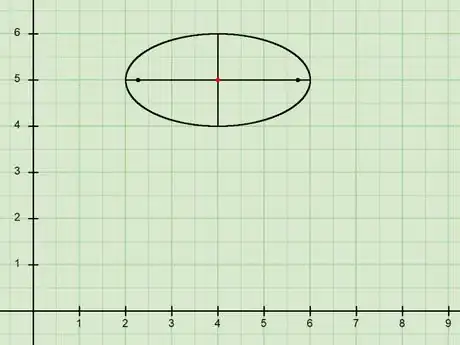
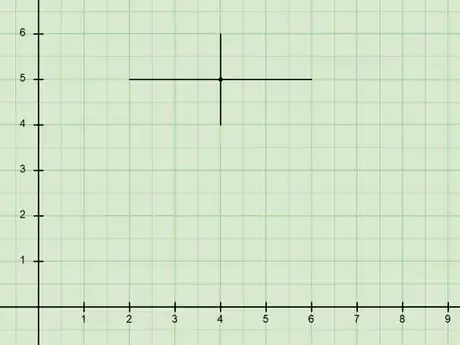
5
Graph the major and minor axes. When doing this, keep in mind that the center is the midpoint of both the major and the minor axes.
- Plot the center of the ellipse that you found earlier (in our example, this was $(4,5)$ ).
- Graph the major axis, taking into account if it's vertical or horizontal (in our example, it was horizontal). If you're having trouble finding if the major axis is vertical or horizontal, take a look at the two possible forms for the ellipse again.
- Graph the minor axis, making it perpendicular to the major axis and passing through the center. Also, the minor axis should be bisected by the major axis.
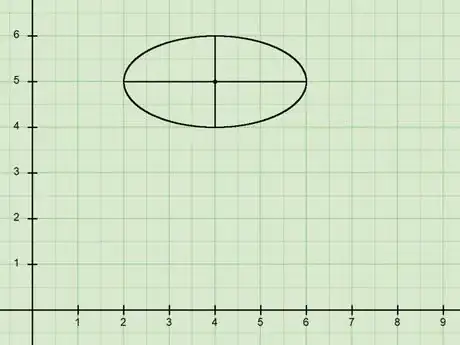
6
Graph the ellipse using the graphs of the major and minor axes. Draw a curve shape passing through the endpoints of the major and minor axes, and you're done!

Tip: Here's how to hand-draw an accurate ellipse!