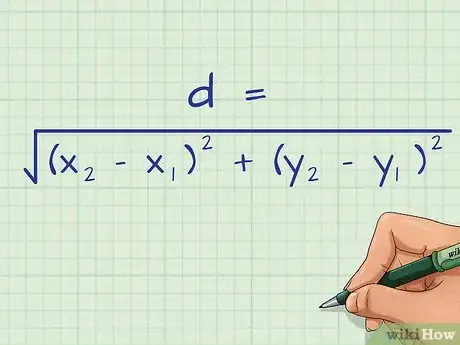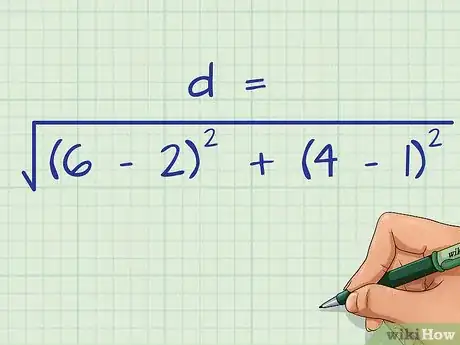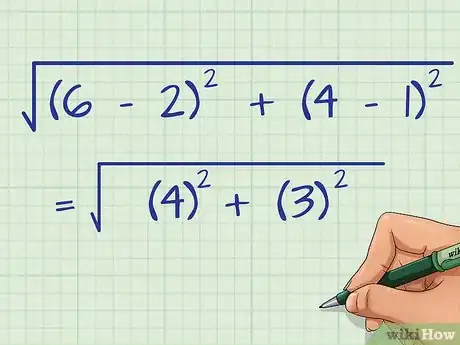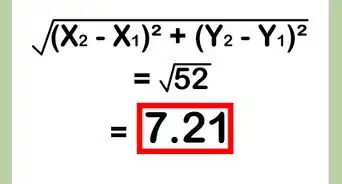How to Use Distance Formula to Find the Length of a Line

Co-authored by wikiHow Staff

Last Updated: March 19, 2023 References

You can measure the length of a vertical or horizontal line on a coordinate plane by simply counting coordinates; however, measuring the length of a diagonal line is trickier. You can use the Distance Formula to find the length of such a line. This formula is basically the Pythagorean Theorem, which you can see if you imagine the given line segment as the hypotenuse of a right triangle.^{[1]
X
Research source} By using a basic geometric formula, measuring lines on a coordinate path becomes a relatively easy task.

Part 1

Part 1 of 2:

Setting up the Formula

1
Set up the Distance Formula. The formula states that $d={\sqrt {(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}}}$ , where $d$ equals the distance of the line, $(x_{1},y_{1})$ equal the coordinates of the first endpoint of the line segment, and $(x_{2},y_{2})$ equal the coordinates of the second endpoint of the line segment.^{[2]
X
Research source}
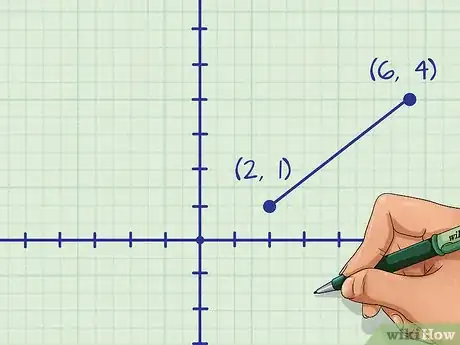
2
Find the coordinates of the line segment’s endpoints. These might already be given. If not, count along the x-axis and y-axis to find the coordinates.^{[3]
X
Research source}
- The x-axis is the horizontal axis; the y-axis is the vertical axis.
- The coordinates of a point are written as $(x,y)$ .
- For example, a line segment might have an endpoint at $(2,1)$ and another at $(6,4)$ .
Advertisement
3
Plug the coordinates into the Distance Formula. Be careful to substitute the values for the correct variables. The two $x$ $x$ coordinates should be inside the first set of parentheses, and the two $y$ $y$ coordinates should be inside the second set of parentheses.^{[4]
X
Research source}
- For example, for points $(2,1)$ and $(6,4)$ , your formula would look like this: $d={\sqrt {(6-2)^{2}+(4-1)^{2}}}$

Part 2

Part 2 of 2:

Calculating the Distance

1
Calculate the subtraction in parentheses. By using the order of operations, any calculations in parentheses must be completed first.^{[5]
X
Research source}
- For example:
  $d={\sqrt {(6-2)^{2}+(4-1)^{2}}}$
  $d={\sqrt {(4)^{2}+(3)^{2}}}$
2
Square the value in parentheses. The order of operations states that exponents should be addressed next.^{[6]
X
Research source}
- For example:
  $d={\sqrt {(4)^{2}+(3)^{2}}}$
  $d={\sqrt {16+9}}$
3
Add the numbers under the radical sign. You do this calculation as if you were working with whole numbers.^{[7]
X
Research source}
- For example:
  $d={\sqrt {16+9}}$
  $d={\sqrt {25}}$
4
Solve for $d$ . To reach your final answer, find the square root of the sum under the radical sign.^{[8]
X
Research source}
- Since you are finding a square root, you may have to round your answer.
- Since you are working on a coordinate plane, your answer will be in generic “units,” not in centimeters, meters, or another metric unit.
- For example:
  $d={\sqrt {25}}$
  $d=5$ units

Community Q&A

Question

What do we call points that are on same line?

Donagan

Top Answerer

Points on the same straight line are said to be "collinear" or "colinear."
Question

How do I simplify the square root?

Donagan

Top Answerer

Look for a perfect square inside the radical sign, find its square root, and put that square root out in front of the radical sign, indicating that it's to be multiplied by the radical. For example: √50 = √(2 x 25) = 5√2.
Question

The rise is 4 inches. The angle is 90 degrees from the height to the base. What is the slope?

Donagan

Top Answerer

To find the slope, you have to know the horizontal distance over which the rise occurs. The 90° angle is not relevant.