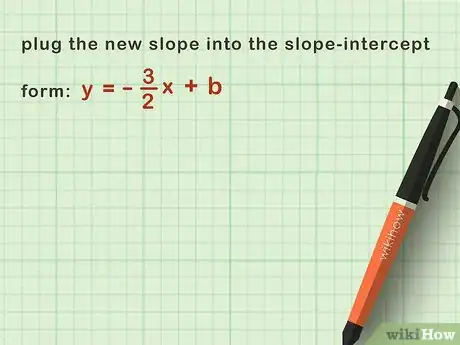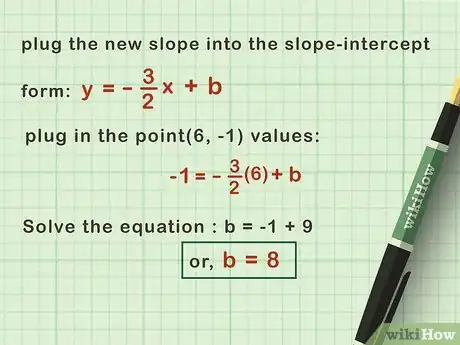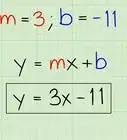This article was co-authored by Grace Imson, MA. Grace Imson is a math teacher with over 40 years of teaching experience. Grace is currently a math instructor at the City College of San Francisco and was previously in the Math Department at Saint Louis University. She has taught math at the elementary, middle, high school, and college levels. She has an MA in Education, specializing in Administration and Supervision from Saint Louis University.
This article has been viewed 118,675 times.
Equations of perpendicular lines are usually introduced in the beginning of geometry or algebra, and are the starting points of many mathematical concepts. Some students may find them complex, but with this guide, you can find perpendicular lines with ease!
Steps
-
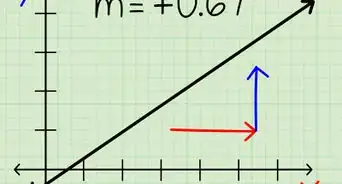
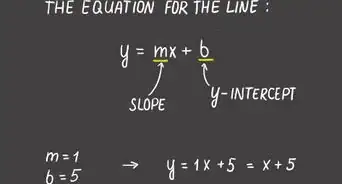
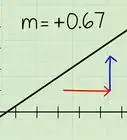
1Identify the equation's slope. In this guide, the slope would be m in slope-intercept form (y=mx+b).[1] The photo above identifies 2/3 as the slope. The slope does not have to be fraction; it can be a whole number.
-
2Change the slope. To change the slope, you must convert the value into its opposite sign (positive to negative or negative to positive). Plus, it must be put into its reciprocal version. The order in which the conversion is done does not matter. Refer to the example above.
- 2/3 becomes -2/3. This makes the slope opposite.
- -2/3 becomes -3/2. This makes the slope both opposite and reciprocal. Thus, the slope has been converted.
Advertisement -
3Write the new equation in slope-intercept form. Replace the old slope with the new slope. Replace the y-intercept's value with a variable (b).
-
4Plug in the point's x- and y-values. This will make the equation ready to be solved. Solving it will lead to the y-intercept's value being found.[2]
-
5Solve the equation. Multiply the new slope with the x-value. Then, cancel out the product (make it become 0) with either addition or subtraction. Don't forget to add or subtract the y-value too. In the end, you should get the y-intercept.
-
6Write the perpendicular line's equation. Still using slope-intercept form, use the new slope and the new y-intercept's value. This is the final answer.
-
7(Optional) Check whether or not your answer is correct. Graph the two equations and measure one of the angles that forms; according to the definition of a perpendicular line, all four angles have to measure 90 degrees.
- If the lines are horizontal and vertical, then they are perpendicular due to the "squares" of the coordinate grid.
Community Q&A
-
QuestionHow do I find the perpendicular bisector between two points?
 DonaganTop Answerer
DonaganTop Answerer