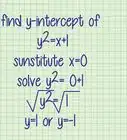How to Graph Sine and Cosine Functions

Last Updated: November 14, 2022

The sine and cosine functions appear all over math in trigonometry, pre-calculus, and even calculus. Understanding how to create and draw these functions is essential to these classes, and to nearly anyone working in a scientific field. This article will teach you how to graph the sine and cosine functions by hand, and how each variable in the standard equations transform the shape, size, and direction of the graphs.

Part 1

Part 1 of 3:

Graphing the Basic Equations

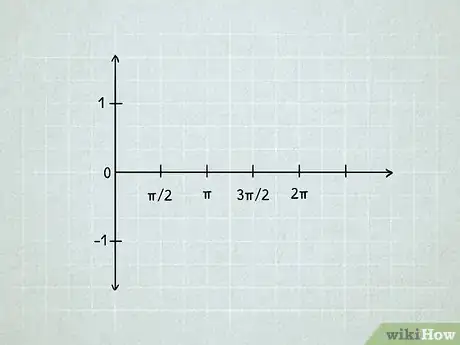
1
Draw a coordinate plane.
- For a sine or cosine graph, simply go from 0 to 2π on the x-axis, and -1 to 1 on the y-axis, intersecting at the origin (0, 0).
- Both $y=\sin(x)$ and $y=\cos(x)$ repeat the same shape from negative infinity to positive infinity on the x-axis (you'll generally only graph a portion of it).
- Use the basic equations as given: $y=\sin(x)$ and $y=cos(x)$
2
Graph the basic form of $y=\sin(x)$ . Plot and connect the points (0, 0), (π/2, 1), (π, 0), and (3π/2, -1) with a continuous curve.
- Both $y=\sin(x)$ and $y=\cos(x)$ never go past -1 or 1 on the y-axis.
- Since you are only hand-drawing your graphs, there is no precise scale, but it must be accurate at certain points.
Advertisement
3
Graph the basic form of $y=cos(x)$ . Plot and connect the points (0, 1), (π/2, 0), (π, -1), and (3π/2, 0) with a continuous curve.
- It may be helpful to use two separate colors to distinguish between sine and cosine.

Part 2

Part 2 of 3:

Graphing Different Sine Equations

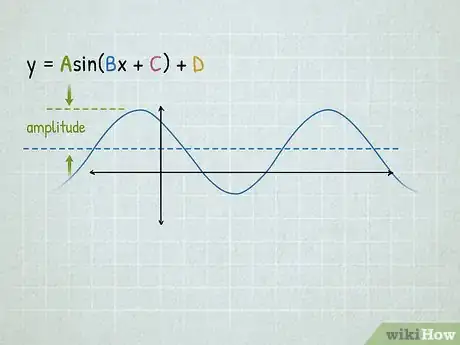
1
Use the standard equation to define your variables. $y=A\sin(Bx+C)+D$ $y=A\sin(Bx+C)+D$
- Find your values of A, B, C, and D.
- Note that in the basic equation for sine, A = 1, B = 1, C = 0, and D = 0.
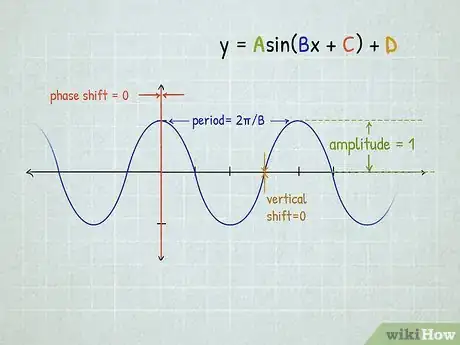
2
Calculate the period.
- Divide your period on the x-axis into four sections that are equal distances apart, just like in the basic equations. The y-values will still alternate from 0, 1, 0, and -1 just like in the basic equation.
- ${\text{Period}}={\frac {2\pi }{B}}$
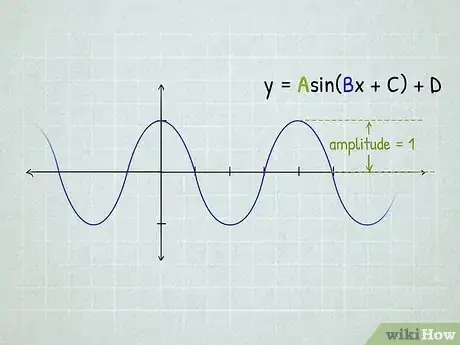
3
Calculate the amplitude.
- ${\text{Amplitude}}=A$
- Multiply the y-values you have by A, and graph these new points.
- If A is negative, the graph will flip over the x-axis. This is called a reflection.
4
Calculate the phase shift.
- ${\text{Phase shift}}={\frac {C}{B}}$
- This will move the graph to the left or right.
- For each x-value in the period, move the x-value to the left by C/B if C/B is negative, or move each x-value to the right by C/B if C/B is positive.
5
Calculate the vertical shift.
- ${\text{Vertical shift}}=D$
- For each y-value, move the y-value up by D if D is positive, or move the y-value down if D is negative.
6
Graph the final function. After each transformation has been applied, your graph is finished!

Part 3

Part 3 of 3:

Graphing Different Cosine Equations

1
Use the standard equation to define your variables. $y=A\cos(Bx+C)+D$ $y=A\cos(Bx+C)+D$
- Find your values of A, B, C, and D.
- Note that in the basic equation for cosine, A = 1, B = 1, C = 0, and D = 0.
2
Calculate the period.
- Divide your period on the x-axis into four sections that are equal distances apart, just like in the basic equations. The y-values will still alternate from 1, 0, -1, and 0 just like in the basic equation.
- ${\text{Period}}={\frac {2\pi }{B}}$
3
Calculate the amplitude.
- ${\text{Amplitude}}=A$
- Multiply the y-values you have by A, and graph these new points.
- If A is negative, the graph will flip over the x-axis. This is called a reflection.
4
Calculate the phase shift.
- ${\text{Phase shift}}={\frac {C}{B}}$
- This will move the graph to the left or right.
- For each x-value in the period, move the x-value to the left by C/B if C/B is negative, or move each x-value to the right by C/B if C/B is positive.
5
Calculate the vertical shift.
- ${\text{Vertical shift}}=D$
- This will move the graph up or down.
- For each y-value, move the y-value up by D if D is positive, or move the y-value down if D is negative.
6
Graph the final function. After each transformation has been applied, your graph is finished!

Warnings

Any negative values for a variable will essentially do the opposite of what a positive variable would do.

⧼thumbs_response⧽
Helpful 1 Not Helpful 0
It is important to calculate the amplitude and period first, because they will make it easier to apply the phase shift and vertical shift later on.

⧼thumbs_response⧽
Helpful 1 Not Helpful 0