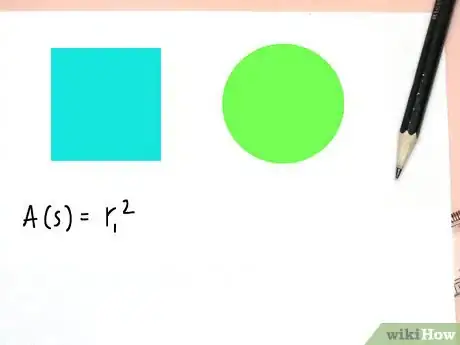X
wikiHow is a “wiki,” similar to Wikipedia, which means that many of our articles are co-written by multiple authors. To create this article, 10 people, some anonymous, worked to edit and improve it over time.
This article has been viewed 145,167 times.
Learn more...
Perhaps you are an artist or interior designer or architect, or perhaps you are into geometry as a discipline of logic. Here is the way to determine a square and circle of equal areas, and further, to understand the meaning of the square root of π. Use r1 to equal the side of a square and r2 to represent the radius of the corresponding circle.
Steps
Part 1
Part 1 of 3:
The Tutorial
-
1Let r1^2 represent the area of the square, A(s).
-
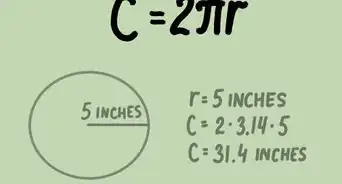
2Let πr2^2 = the area of the circle, A(c).Advertisement
-
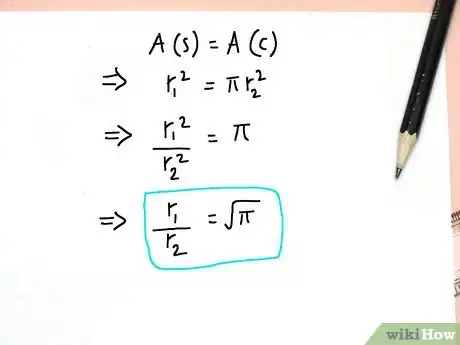
3Set A(s) = A(c) via r1^2 = πr2^2.
-
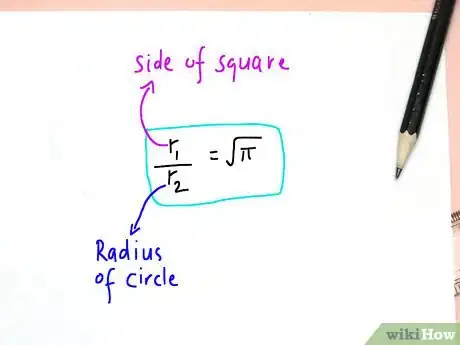
4Then r1^2 / r2^2 = π and r1 / r2 = sqrt(π).
-
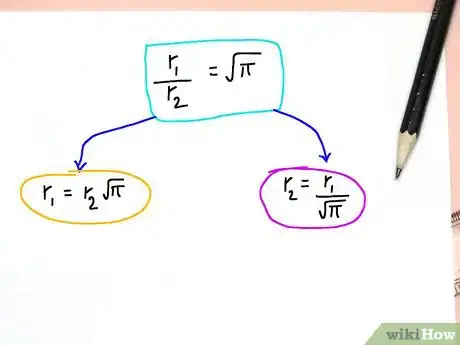
5Given either r1 or r2, we can determine the other one. That is: r1 = sqrt(π)*r2 and r2 = r1/sqrt(π). sqrt(π) = 1.77245385090552. So, given a square of side r1 = 1.77245385090552, its area = 1.77245385090552^2 = π and r2 = r1/sqrt(π) or 1.77245385090552/1.77245385090552 = 1 and the area of r2's circle = πr2^2 = π(1)^2 = π, which equals the area of the square just calculated.
-
6And it's been learned that the square root of π means the relationship between the equal areas of a square and circle of varying "radius."
Advertisement
Part 3
Part 3 of 3:
Helpful Guidance
-
1Make use of helper articles when proceeding through this tutorial:
- See the article How to Determine a Square and Circle of Equal Perimeter for a list of articles related to Excel, Geometric and/or Trigonometric Art, Charting/Diagramming and Algebraic Formulation.
- For more art charts and graphs, you might also want to click on Category:Microsoft Excel Imagery, Category:Mathematics, Category:Spreadsheets or Category:Graphics to view many Excel worksheets and charts where Trigonometry, Geometry and Calculus have been turned into Art, or simply click on the category as appears in the upper right white portion of this page, or at the bottom left of the page.
-
2
Advertisement
Community Q&A
-
QuestionIf area of circle is equal to the area of square, then what is the relation between circumference (c) and perimeter (p) of the square?
 DonaganTop AnswererThe relationship is that the perimeter of the square is equal to the circumference of the circle multiplied by 1.13. Thus, p = 1.13 c. Here's how that's derived: the circle's area (πr²) is defined as being equal to the square's area (4s), where r is the circle's radius, and s is the square's side. So πr² = s², making s equal to r√π. The square's perimeter is 4s, or 4r√π. You would have to multiply the circumference (2πr) by (2/√π), or 1.13, to get the square's perimeter (4r√π). So the relationship of circumference to perimeter is p = 1.13 c. This is true only when the two areas are equal.
DonaganTop AnswererThe relationship is that the perimeter of the square is equal to the circumference of the circle multiplied by 1.13. Thus, p = 1.13 c. Here's how that's derived: the circle's area (πr²) is defined as being equal to the square's area (4s), where r is the circle's radius, and s is the square's side. So πr² = s², making s equal to r√π. The square's perimeter is 4s, or 4r√π. You would have to multiply the circumference (2πr) by (2/√π), or 1.13, to get the square's perimeter (4r√π). So the relationship of circumference to perimeter is p = 1.13 c. This is true only when the two areas are equal. -
QuestionWhat is the area of circle whose radius is the diagonal of a square whose area is 4 cm square?
 DonaganTop AnswererA square with an area of 4 cm² has sides of 2 cm each and a diagonal of 2√2 cm. A circle whose radius is 2√2 cm has an area of π(2√2)² = 8π = 25.13 cm².
DonaganTop AnswererA square with an area of 4 cm² has sides of 2 cm each and a diagonal of 2√2 cm. A circle whose radius is 2√2 cm has an area of π(2√2)² = 8π = 25.13 cm². -
QuestionIf area of a square is A, how do I find the area of circle using same perimeter?
 DonaganTop AnswererIf the square's area is A, each side is √A. So the square's perimeter is 4√A, and so is the circle's circumference. Then the diameter of the circle is its circumference divided by pi, or (4√A) / π, meaning its radius is (2√A) / π. Then the circle's area is πr², or π(2√A / π)² = 4A / π² = (0.405)(A), or (.4A).
DonaganTop AnswererIf the square's area is A, each side is √A. So the square's perimeter is 4√A, and so is the circle's circumference. Then the diameter of the circle is its circumference divided by pi, or (4√A) / π, meaning its radius is (2√A) / π. Then the circle's area is πr², or π(2√A / π)² = 4A / π² = (0.405)(A), or (.4A).
Advertisement
References
- The source workbook for this article is "AREAS equal.xlsx".
About This Article
Advertisement