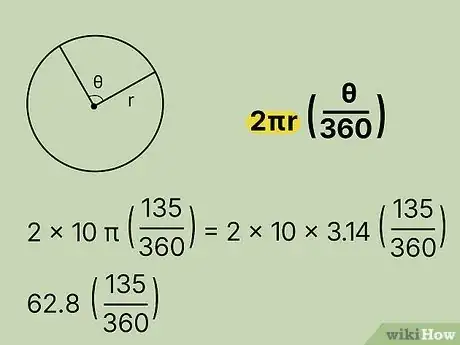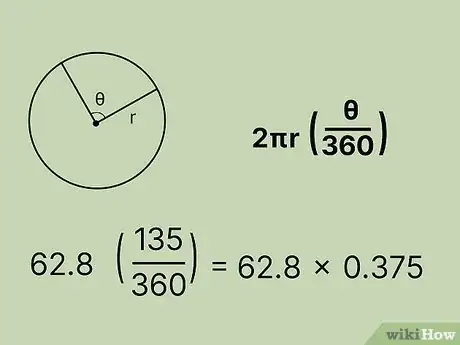2 Different Ways to Find a Circle’s Arc Length

Determining the arc length of a circle is easy with these simple formulas

Co-authored by Mario Banuelos, PhD and Devin McSween

Last Updated: March 15, 2023

Solving When the Central Angle is in Degrees

|

Solving When the Central Angle is in Radians

|

Practice Problems and Answers

|

Video

|

Expert Q&A

|

Tips

If you’re learning about arc lengths in geometry, your teacher probably just assigned you a bunch of problems for homework. You’ve got the circle’s radius and the central angle, so how do you find the length of the arc? Well, you’ve come to the right place! Arc length is the distance between one endpoint of an arc on a circle to the other. In this article, we’ll tell you what formulas you need and how to use them to find a circle's arc length. Read on to learn more!

Things You Should Know

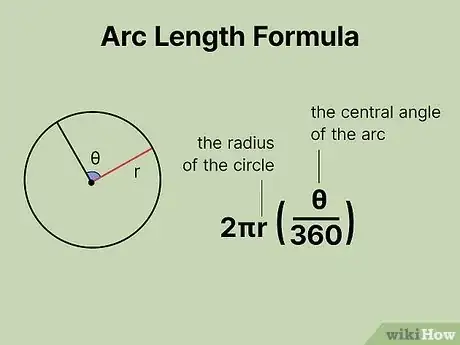
When the circle’s central angle is measured in degrees, use the formula ${\text{arc length}}=2\pi (r)({\frac {\theta }{360}})$ .
If the central angle is in radians, use the formula ${\text{arc length}}=\theta (r)$ .
Plug in the circle’s radius and the central angle’s measurement to solve either formula.

Method 1

Method 1 of 2:

Solving When the Central Angle is in Degrees

1
Set up the formula for arc length. The formula is ${\text{arc length}}=2\pi (r)({\frac {\theta }{360}})$ , where $r$ equals the radius of the circle and $\theta$ equals the measurement of the arc’s central angle, in degrees.^{[1]
X
Expert Source

Mario Banuelos, PhD
Assistant Professor of Mathematics
Expert Interview. 19 January 2021.}
2
Plug the length of the circle’s radius into the formula. This information is typically given to you in a problem. Otherwise, measure the circle’s radius with a ruler or protractor. Simply substitute the radius’ value for the variable $r$ $r$ .
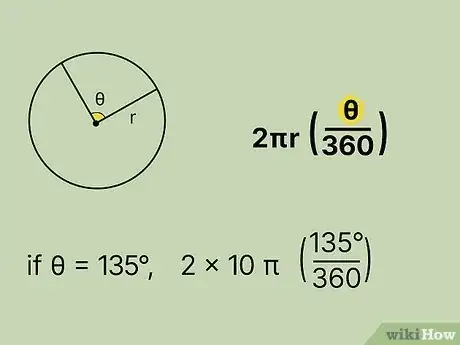
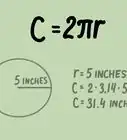
- For example, if the circle’s radius is 10 cm, set up the formula like this: ${\text{arc length}}=2\pi (10)({\frac {\theta }{360}})$ .
Advertisement
3
Insert the value of the arc’s central angle into the formula. Typically, the problem you’re working on provides this information. Make sure to convert the angle to degrees if it’s currently in radians. Then, substitute the central angle’s measurement for $\theta$ $\theta$ in the formula.
- For example, if the arc’s central angle is 135 degrees, your formula now looks like: ${\text{arc length}}=2\pi (10)({\frac {135}{360}})$ .
4
Multiply the radius by $2\pi$ . If you are not using a calculator, use the approximation $\pi =3.14$ $\pi =3.14$ for your calculations. Rewrite the formula using this new value, which represents the circle’s circumference.^{[2]
X
Research source}
- For example, your formula now looks like:
  ${\text{arc length}}=2\pi (10)({\frac {135}{360}})$
  $=2(3.14)(10)({\frac {135}{360}})$
  $=(62.8)({\frac {135}{360}})$
5
Divide the arc’s central angle by 360 degrees. Since a circle has 360 degrees total, dividing the central angle by 360 degrees gives you the portion of the circle that the sector represents. Using this information, find what portion of the circumference the arc length represents.
- For example, simplify the formula to get:
  ${\text{arc length}}=(62.8)({\frac {135}{360}})$
  $=(62.8)(.375)$
6
Multiply the two numbers together. This gives you the length of the arc.
- Solve the formula:
  ${\text{arc length}}=(62.8)(.375)=23.55$
  So, the arc length of a circle with a radius of 10 cm and a central angle of 135 degrees is about 23.55 cm.

Method 2

Method 2 of 2:

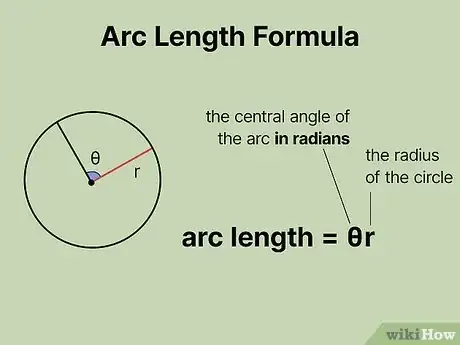
Solving When the Central Angle is in Radians

1
Set up the formula for arc length. The formula is ${\text{arc length}}=\theta (r)$ , where $\theta$ equals the arc’s central angle in radians, and $r$ equals the length of the circle’s radius.^{[3]
X
Research source}
2
Plug the length of the circle’s radius into the formula. The math problem you’re working on typically provides this information. Just substitute the length of the radius for the variable $r$ $r$ .
- For example, if the circle’s radius is 10 cm, your formula looks like this: ${\text{arc length}}=\theta (10)$ .
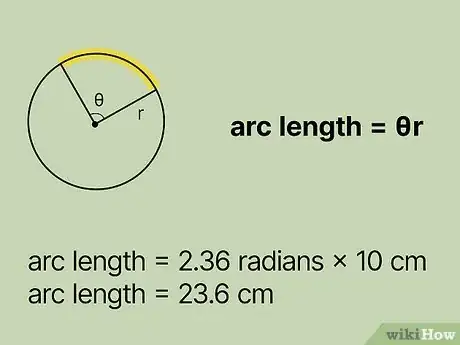
3
Plug the measurement of the arc’s central angle into the formula. When using this formula, the arc’s central angle needs to be in radians. If the central angle is in degrees, just convert it into radians.
- For example, if the arc’s central angle is 2.36 radians, your formula now looks like this: ${\text{arc length}}=2.36(10)$ .
4
Multiply the radius by the arc’s central angle. The product gives you the length of the arc.
- For example:
  ${\text{arc length}}=2.36(10)=23.6$
  So, the length of an arc of a circle with a radius of 10 cm and a central angle of 23.6 radians, is about 23.6 cm.

Practice Problems and Answers

Practice Problems and Answers to Find Arc Length

Expert Q&A
Did you know you can get premium answers for this article? Unlock premium answers by supporting wikiHow

Question

How do you calculate the length of an arc?

Mario Banuelos, PhD
Assistant Professor of Mathematics
Mario Banuelos is an Assistant Professor of Mathematics at California State University, Fresno. With over eight years of teaching experience, Mario specializes in mathematical biology, optimization, statistical models for genome evolution, and data science. Mario holds a BA in Mathematics from California State University, Fresno, and a Ph.D. in Applied Mathematics from the University of California, Merced. Mario has taught at both the high school and collegiate levels.

Mario Banuelos, PhD

Assistant Professor of Mathematics

Expert Answer

Support wikiHow by unlocking this expert answer.

To find the arc length, set up the formula Arc length = 2 x pi x radius x (arc's central angle/360), where the arc's central angle is measured in degrees.
Question

How do l find the arc length if I'm not given the central angle?

wikiHow Staff Editor
Staff Answer
This answer was written by one of our trained team of researchers who validated it for accuracy and comprehensiveness.

wikiHow Staff Editor

Staff Answer

Support wikiHow by unlocking this staff-researched answer.

If you're not given the central angle, you'll typically be given the sector area of the arc. To find the arc length with a sector area, multiply the sector area by 2. Then, divide the product by the radius squared ((SA*2)/r^2). Your answer gives you the central angle in radians. You now have the central angle in radians, so simply multiply the central angle by the radius to find the arc length.
Question

Is the measurement of an inscribed angle half the measurement of the central angle that intercepts the same arc?

wikiHow Staff Editor
Staff Answer
This answer was written by one of our trained team of researchers who validated it for accuracy and comprehensiveness.

wikiHow Staff Editor

Staff Answer

Support wikiHow by unlocking this staff-researched answer.

That is correct. The vertex of an inscribed angle is on the outside of a circle. When an inscribed angle and a central angle share the same arc on a circle, the inscribed angle is equal to half of the measure of the central angle. The inscribed angle is also equal to half the measure of the arc.