How to Find the Area of a Circle Using Its Circumference

Last Updated: September 26, 2022

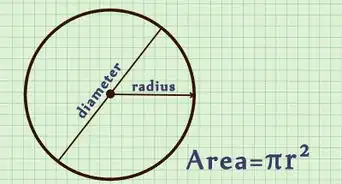
Finding the area of a circle is a straightforward calculation if you know the length of the circle’s radius. If you don’t know the radius, however, you can still calculate the area if you are given the length of the circle’s circumference or perimeter. You can use a two-step process, solving first for the radius using the formula for the circumference: ${\text{circumference}}=2\pi (r)$ . Then you can use the formula ${\text{area}}=\pi (r^{2})$ to find the area. You can also use the formula ${\text{circumference}}=2{\sqrt {\pi (A)}}$ , which expresses the circumference of a circle as a function of its area, without knowing the length of the radius at all.

Part 1

Part 1 of 3:

Finding the Radius Given the Circumference

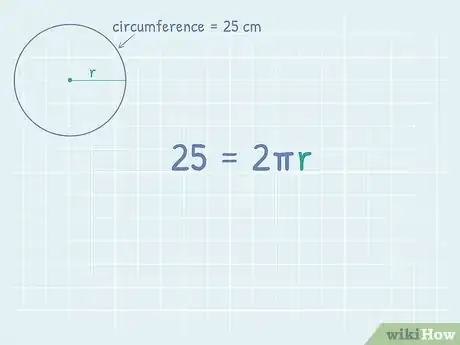
1
Set up the formula for finding the circumference of a circle. The formula is ${\text{circumference}}=2\pi (r)$ , where $r$ equals the radius of the circle.^{[1]
X
Research source} Using this formula allows you to find the length of the radius, which can in turn be used to find the area of the circle.
2
Plug the circumference into the formula. Make sure you substitute the value on the left side of the equation, not for the variable $r$ $r$ . If you don’t know the circumference, you cannot use this method.
- For example, if you know the circumference of a circle is 25 centimeter (9.8 in), your formula will look like this: $25=2\pi (r)$ .
Advertisement
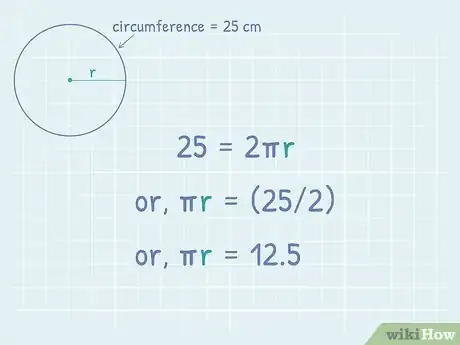
3
Divide both sides of the equation by 2. This will cancel the coefficient of 2 on the right side of the equation, leaving you with $\pi (r)$ $\pi (r)$ .
- For example:
  $25=2\pi (r)$
  ${\frac {25}{2}}={\frac {2\pi (r)}{2}}$
  $12.5=\pi (r)$
4
Divide both sides of the equation by 3.14. This is the generally accepted rounded value of $\pi$ $\pi$ . You can also use the $\pi$ $\pi$ function on a scientific calculator for a more exact result. Dividing by $\pi$ $\pi$ isolates the radius, giving you its value.^{[2]
X
Research source}
- For example:
  $12.5=\pi (r)$
  ${\frac {12.5}{\pi }}={\frac {\pi (r)}{\pi }}$
  $3.98=r$

Part 2

Part 2 of 3:

Finding the Area Given the Radius

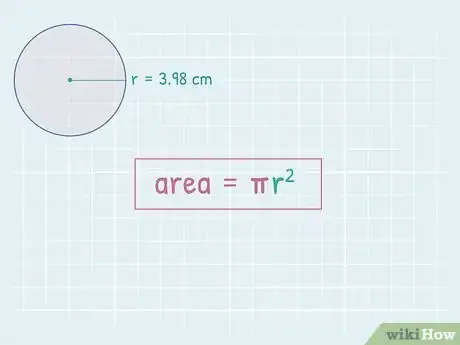
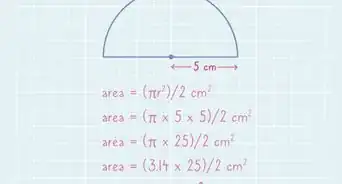
1
Set up the formula for finding the area of a circle. The formula is ${\text{area}}=\pi (r^{2})$ , where $r$ equals the radius of the circle.^{[3]
X
Expert Source

Grace Imson, MA
Math Instructor, City College of San Francisco
Expert Interview. 1 November 2019.} Don’t confuse the formula for area with the formula for circumference, which you previously used to calculate the radius.
2
Plug the radius into the formula. Substitute the value you previously calculated and substitute it for the variable $r$ $r$ . Then, square the value. To square a value means to multiply it by itself. It’s easy to do this using the $x^{2}$ $x^{{2}}$ button on a scientific calculator.
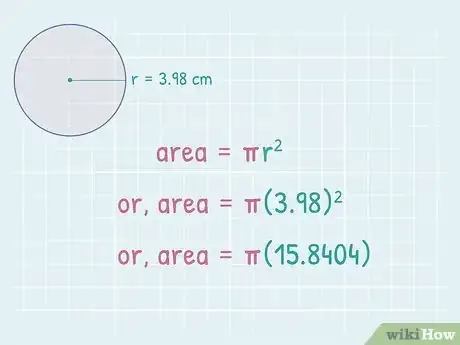
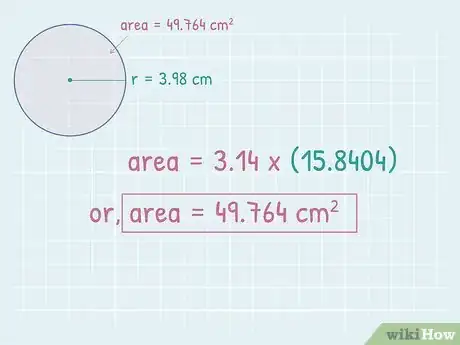
- For example, if you found the radius to be 3.98, you would calculate:
  ${\text{area}}=\pi (r^{2})$
  ${\text{area}}=\pi (3.98^{2})$
  ${\text{area}}=\pi (15.8404)$
3
Multiply by $\pi$ . If you are not using a calculator, you can use the rounded value 3.14 for $\pi$ $\pi$ . The product will give you the area of the circle, in square units.^{[4]
X
Research source}
- For example:
  ${\text{area}}=\pi (15.8404)$
  ${\text{area}}=49.764$
  So, the area of a circle with a circumference of 25 centimeter (9.8 in) is about 49.764 square centimeters.

Part 3

Part 3 of 3:

Using a Formula Given the Circumference

1
Set up the formula for the circumference of a circle, as a function of its area. The formula is ${\text{circumference}}=2{\sqrt {\pi (A)}}$ , where $A$ equals the area of the circle. This formula is derived by rearranging the value of $r$ in the formula for the area of a circle ( ${\text{area}}=\pi (r^{2})$ ) and substituting that value into the circumference formula ( ${\text{circumference}}=2\pi (r)$ ).^{[5]
X
Research source}
2
Plug the circumference into the formula. This information should be given to you. Make sure you substitute the circumference on the left side of the formula, not for the value of $A$ $A$ on the right side.
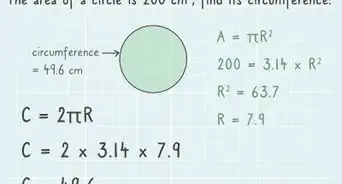
- For example, if you know the circumference is 25 centimeter (9.8 in), your formula will look like this: $25=2{\sqrt {\pi (A)}}$ .
3
Divide both sides of the equation by 2. Remember that what you do to one side of an equation, you must do to the other side as well. Dividing by 2 simplifies the right side to ${\sqrt {\pi (A)}}$ ${\sqrt {\pi (A)}}$ .
- For example:
  $25=2{\sqrt {\pi (A)}}$
  ${\frac {25}{2}}={\frac {2{\sqrt {\pi (A)}}}{2}}$
  $12.5={\sqrt {\pi (A)}}$
4
Square both sides of the equation. When you square a value, you multiply the value by itself. Squaring a square root cancels the square root, leaving you with the value under the radical sign. Remember to keep the equation balanced by squaring both sides.
- For example:
  $12.5={\sqrt {\pi (A)}}$
  $12.5^{2}=({\sqrt {\pi (A)}})^{2}$
  $156.25=\pi (A)$
5
Divide each side of the equation by 3.14. If you have a scientific calculator, you can use the $\pi$ $\pi$ function instead to get a more accurate answer. This will cancel out $\pi$ $\pi$ on the right side of the equation, leaving you with the value of $A$ $A$ . This is the area of the circle, in square units.
- For example:
  $156.25=\pi (A)$
  ${\frac {156.25}{\pi }}={\frac {\pi (A)}{\pi }}$
  $49.7359=A$
  So, the area of a circle with a circumference of 25 centimeter (9.8 in) is about 49.74 square centimeters.

Community Q&A

Question

I still don't get it. Can you explain it easier?

Donagan

Top Answerer

Divide the circumference by 3.14 (pi): that gives you the diameter. Divide by 2: that gives you the radius. Square the radius, and multiply that by pi: that gives you the area.
Question

If a circle circumference is 48 inches pi, what is the area in square inches?

Donagan

Top Answerer

If the circumference (πd) is 48π, the diameter is 48 inches. That makes the radius 24 inches, and the area is πr² = 576π = 1,808.64 square inches.