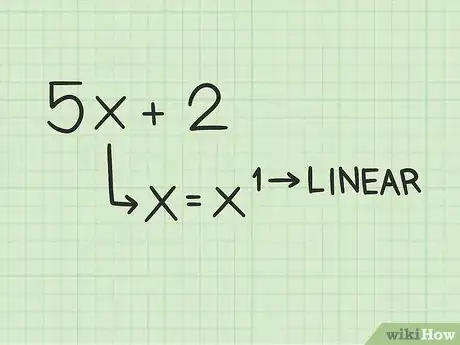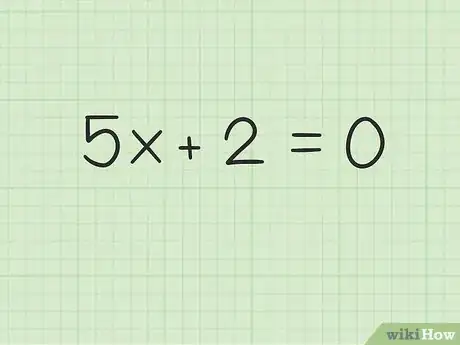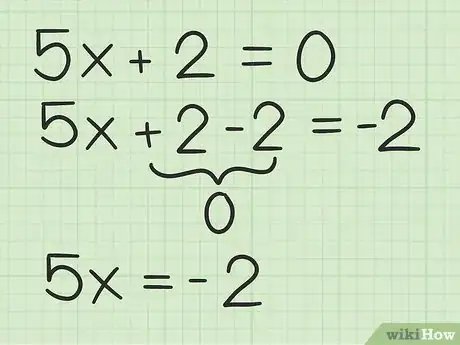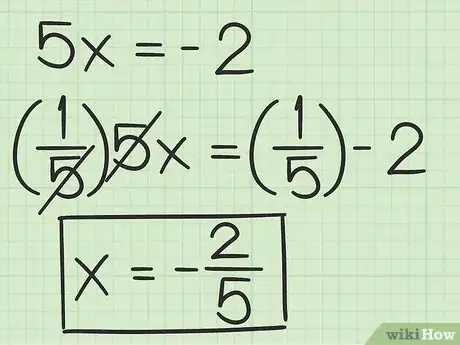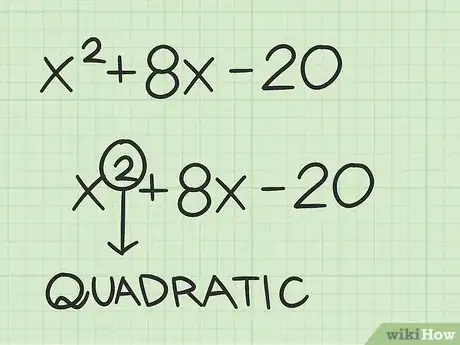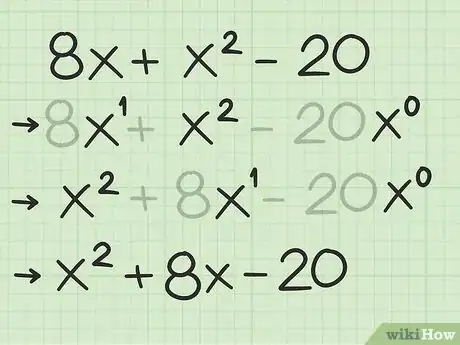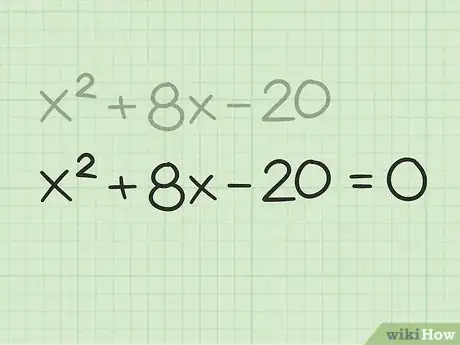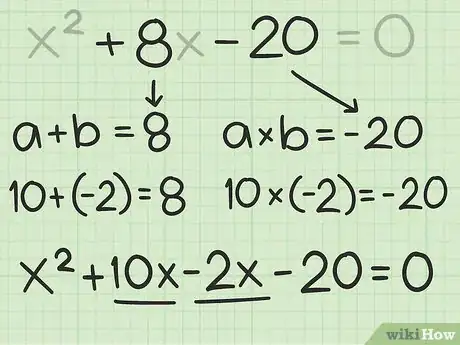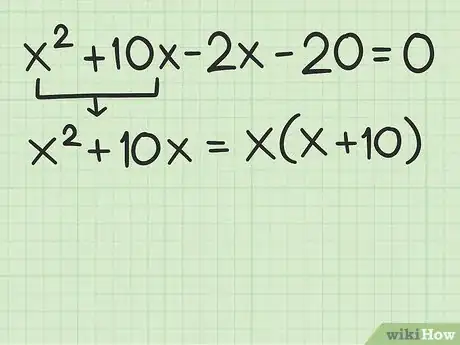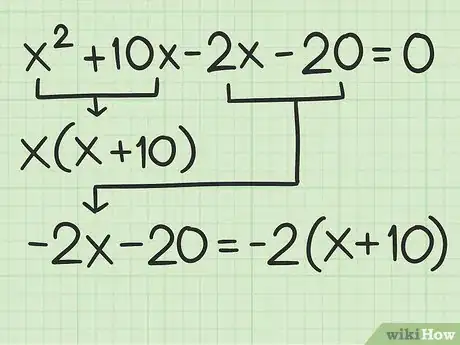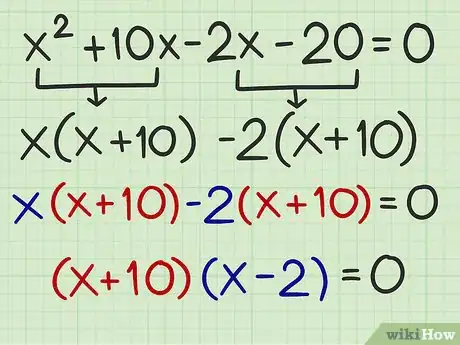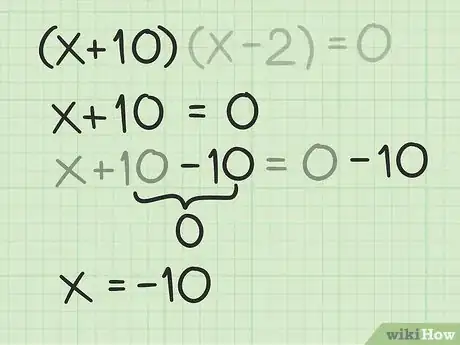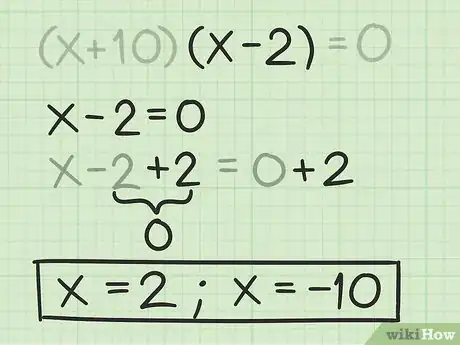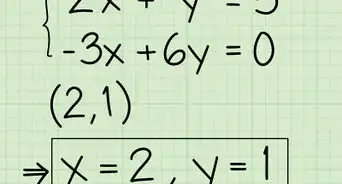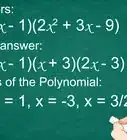This article was co-authored by David Jia. David Jia is an Academic Tutor and the Founder of LA Math Tutoring, a private tutoring company based in Los Angeles, California. With over 10 years of teaching experience, David works with students of all ages and grades in various subjects, as well as college admissions counseling and test preparation for the SAT, ACT, ISEE, and more. After attaining a perfect 800 math score and a 690 English score on the SAT, David was awarded the Dickinson Scholarship from the University of Miami, where he graduated with a Bachelor’s degree in Business Administration. Additionally, David has worked as an instructor for online videos for textbook companies such as Larson Texts, Big Ideas Learning, and Big Ideas Math.
There are 12 references cited in this article, which can be found at the bottom of the page.
This article has been viewed 299,264 times.
A polynomial is an expression made up of adding and subtracting terms. A terms can consist of constants, coefficients, and variables. When solving polynomials, you usually trying to figure out for which x-values y=0. Lower-degree polynomials will have zero, one or two real solutions, depending on whether they are linear polynomials or quadratic polynomials. These types of polynomials can be easily solved using basic algebra and factoring methods. For help solving polynomials of a higher degree, read Solve Higher Degree Polynomials.
Steps
Solving a Linear Polynomial
-
1Determine whether you have a linear polynomial. A linear polynomial is a polynomial of the first degree.[1] This means that no variable will have an exponent greater than one. Because this is a first-degree polynomial, it will have exactly one real root, or solution.[2]
- For example, is a linear polynomial, because the variable has no exponent (which is the same as an exponent of 1).
-
2Set the equation to equal zero. This is a necessary step for solving all polynomials.[3]
- For example,
Advertisement -
3
-
4Solve for the variable. Usually you will need to divide each side of the equation by the coefficient. This will give you the root, or solution, to your polynomial.[6]
- For example, to solve for in , you would divide each side of the equation by :
So, the solution to is .
- For example, to solve for in , you would divide each side of the equation by :
Solving a Quadratic Polynomial
-
1Determine whether you have a quadratic polynomial. A quadratic polynomial is a polynomial of the second degree.[7] This means that no variable will have an exponent greater than 2. Because this is a second-degree polynomial, it will have two real roots, or solutions.[8]
- For example, is a quadratic polynomial, because the variable has an exponent of .
-
2Make sure the polynomial is written in order of degree. This means that the term with the exponent of is listed first, followed by the first-degree term, followed by the constant.[9]
- For example, you would rewrite as .
-
3Set the equation to equal zero. This is a necessary step for solving all polynomials.[10]
- For example, .
-
4Rewrite the expression as a four-term expression. To do this, split up the first-degree term (the term). You are looking for two numbers whose sum is equal to the first degree coefficient, and whose product is equal to the constant. [11]
- For example, for the quadratic polynomial , you need to find two numbers ( and ), where , and .
- Since you have , you know that one of the number will be negative.
- You should see that and . Thus, you will split up into and rewrite the quadratic polynomial: .
-
5Factor by grouping. To do this, factor out a term common to the first two terms in the polynomial.[12]
- For example, the first two terms in the polynomial are . A term common to both is . Thus, the factored group is .
-
6Factor the second group. To do this, factor out a term common to the second two terms in the polynomial.[13]
- For example, the second two terms in the polynomial are . A term common to both is . Thus, the factored group is .
-
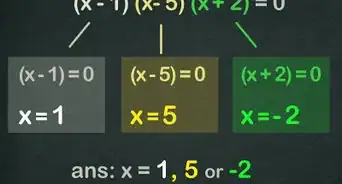
7Rewrite the polynomial as two binomials. A binomial is a two-term expression. You already have one binomial, which is the expression in parentheses for each group. This expression should be the same for each group. The second binomial is created by combining the two terms that were factored out of each group.[14]
- For example, after factoring by grouping, becomes .
- The first binomial is .
- The second binomial is .
- So the original quadratic polynomial, can be written as the factored expression .
-
8Find the first root, or solution. To do this, solve for in the first binomial.[15]
- For example, to find the first root for , you would first set the first binomial expression to and solve for . Thus:
So, the first root of the quadratic polynomial is .
- For example, to find the first root for , you would first set the first binomial expression to and solve for . Thus:
-
9Find the second root, or solution. To do this, solve for in the second binomial.[16]
- For example, to find the second root for , you would set the second binomial expression to and solve for . Thus:
So, the second root of the quadratic polynomial is .
- For example, to find the second root for , you would set the second binomial expression to and solve for . Thus:
Community Q&A
-
QuestionHow did you get -2 in the second binomial?
 DonaganTop AnswererThe original equation was 5x + 2 = 0. Then 2 was subtracted from both sides of the equation in order to begin the process of solving for x. This resulted in 5x = -2.
DonaganTop AnswererThe original equation was 5x + 2 = 0. Then 2 was subtracted from both sides of the equation in order to begin the process of solving for x. This resulted in 5x = -2. -
QuestionWhat do I get if I add x - 2 and 1/x?
 DonaganTop AnswererYou get x - 2 + 1/x.
DonaganTop AnswererYou get x - 2 + 1/x. -
QuestionFor trinomials, would I turn them into a quadratic polynomials and then binomials?
 Community AnswerYes. To factor a trinomial, you must split it into a quadratic polynomial.
Community AnswerYes. To factor a trinomial, you must split it into a quadratic polynomial.
References
- ↑ https://www.cuemath.com/algebra/linear-polynomial/
- ↑ https://www.math.utah.edu/~wortman/1050-text-calp.pdf
- ↑ https://www.mathsisfun.com/algebra/polynomials-solving.html
- ↑ David Jia. Academic Tutor. Expert Interview. 7 January 2021.
- ↑ http://www.mathwords.com/c/constant.htm
- ↑ https://www.cuemath.com/algebra/linear-polynomial/
- ↑ https://www.cuemath.com/algebra/factorization-of-quadratic-polynomials/
- ↑ http://www.themathpage.com/aprecalc/quadratic-equation.htm#double
- ↑ https://www.math.utah.edu/~wortman/1050-text-qp.pdf
- ↑ https://www.cuemath.com/algebra/factorization-of-quadratic-polynomials/
- ↑ https://www.khanacademy.org/math/algebra/quadratics/solving-quadratic-equations-by-factoring/v/example-1-solving-a-quadratic-equation-by-factoring
- ↑ https://www.khanacademy.org/math/algebra/x2f8bb11595b61c86:quadratics-multiplying-factoring/x2f8bb11595b61c86:factor-quadratics-grouping/a/factoring-by-grouping
- ↑ https://www.khanacademy.org/math/algebra/x2f8bb11595b61c86:quadratics-multiplying-factoring/x2f8bb11595b61c86:factor-quadratics-grouping/a/factoring-by-grouping
- ↑ https://www.khanacademy.org/math/algebra/x2f8bb11595b61c86:quadratics-multiplying-factoring/x2f8bb11595b61c86:factor-quadratics-grouping/a/factoring-by-grouping
- ↑ https://www.khanacademy.org/math/algebra/quadratics/solving-quadratic-equations-by-factoring/v/example-1-solving-a-quadratic-equation-by-factoring
- ↑ https://www.khanacademy.org/math/algebra/quadratics/solving-quadratic-equations-by-factoring/v/example-1-solving-a-quadratic-equation-by-factoring
- ↑ https://content.byui.edu/file/b8b83119-9acc-4a7b-bc84-efacf9043998/1/Math-1-6-1.html
About This Article
To solve a linear polynomial, set the equation to equal zero, then isolate and solve for the variable. A linear polynomial will have only one answer. If you need to solve a quadratic polynomial, write the equation in order of the highest degree to the lowest, then set the equation to equal zero. Rewrite the expression as a 4-term expression and factor the equation by grouping. Rewrite the polynomial as 2 binomials and solve each one. If you want to learn how to simplify and solve your terms in a polynomial equation, keep reading the article!