This article was co-authored by wikiHow Staff. Our trained team of editors and researchers validate articles for accuracy and comprehensiveness. wikiHow's Content Management Team carefully monitors the work from our editorial staff to ensure that each article is backed by trusted research and meets our high quality standards.
There are 10 references cited in this article, which can be found at the bottom of the page.
This article has been viewed 474,141 times.
Learn more...
Radicals, also called roots, are the opposite of exponents. They even sound like opposites when we're talking about them out loud: we say is "six squared", and is "the square root of six". And just like we can use larger and larger exponents like and , we can also find smaller and smaller roots like and . Simplifying radical expressions uses many of the same tricks you've learned in earlier math lessons for simplifying fractions or exponents. If you're new to the topic, start by learning how to simplify the square root of an integer.
Steps
Simplifying the Square Root of an Integer
-
1Factor the number under the square root. Ignore the square root for now and just look at the number underneath it. Factor that number by writing it as the product of two smaller numbers. (If the factors aren't obvious, just see if it divides evenly by 2. If not, try again with 3, then 4, and so on, until you find a factor that works.)[1]
- Example: Simplify .
- The first step is finding some factors of 45. You can't divide 45 by 2, so try dividing it by 3 instead: , so .
-
2Keep going until the number is factored completely. Remember, any number can be factored down into prime numbers (like 2, 3, 5, and 7). Keep breaking down the factors until there are no more factors to find.[2]
- Now we have , but we can factor 15 again into .
Advertisement -
3Rewrite pairs of the same number as powers of 2. If the same factor shows up more than once, rewrite it as an exponent. (Keep everything underneath the square root.)[3]
- In , the number 3 shows up twice. Since , we can rewrite the whole expression as .
-
4Take any numbers raised to the power of 2 outside the square root. Roots and exponents are opposite, so they cancel each other out. If any factors are raised to the power of 2, move that factor in front of the square root (and get rid of the exponent).[4]
- (As long as everything underneath the root is one multiplication problem, you can always rewrite the expression like this, with a root over each product.)
- Since there are no other exponents left under the square root, you're all done!
-
5Simplify the result so there is no multiplication left. In more difficult problems, you might end up with multiple numbers in front of the square root, or underneath it. Solve these multiplication problems to simplify the answer.
- Example: Simplify .
- This takes a lot of factoring to break down:
- Rewrite pairs of numbers using exponents: .
- Bring the 2 and 3 outside the square root:
- Simplify the numbers in front of the square root:
- To get the final answer, simplify the numbers under the square root:
Simplifying Cube Roots and Higher Roots
-
1Find the prime factors of the number under the root. Just like square roots, the first step to simplifying a cube root (), a fourth root (), or any higher root is to factor the number under the root.[5]
- Example: Simplify (the cube root of 81).
- , so
-
2Rewrite groups of the same factors in exponent form. If the same prime factor shows up more than once, rewrite them as an exponent.[6]
-
3Simplify the root of exponents wherever possible. Just as a square root cancels out a square, higher roots cancel out matching exponents (for instance, and ). Check out this example to see how this works:[7]
- Since the root and exponent match in , they cancel out, leaving only the base number, .
- Plug that into the whole expression to get . Since there are no more exponents left that can cancel out, this is the simplified form.
-
4Simplify any multiplication and exponents. You'll often end up with exponents that don't cancel out, or with more than one number multiplied together. Solve for these so you end up with one number outside the radical, and one number inside it.
- Example: Simplify .
- This is already factored into prime numbers, so we can skip that step. Let's rewrite this as .
- , by the rules of exponents. The root and exponent cancel out in the first term, leaving
- In , the root and exponent cancel out to make .
- Since has no exponents that cancel out, this can't be simplified.
- Plug your simplified terms back into the whole expression:
- Combine like terms:
- Calculate multiplication and exponents:
Simplifying Fractions inside Roots
-
1Simplify the fraction. What if a whole fraction is underneath a root? One way to solve problems like this is to ignore the radical expression at first. Simplify the fraction as much as you can, then see if the root lets you simplify further.[8]
- Example: Simplify .
- , so we can rewrite this as .
- , so .
-
2Rewrite the fraction as two radical expressions instead. Some people prefer this other method of solving problems like this. Rewrite the fraction so there is one root in the numerator and another in the denominator. Simplify each root separately, then simplify the fraction.[9]
- Example: Simplify .
- Rewrite this as .
- Simplify the numerator:
- Simplify the denominator:
- Plug these back into the fraction:
- Cancel out to get .
-
3Adjust your answer so there are no roots in the denominator. Sometimes, the simplest form still has a radical expression. That's fine, but most math teachers want you to keep any radicals in the top of the fraction, not the denominator. Follow the rules for multiplying fractions to cancel out any roots on the bottom of your fraction:[10]
- Example: You've simplified a fraction and got the answer .
- To put it in standard form, multiply the top and bottom of the fraction by the root:
Combining Roots of Different Kinds
-
1Convert roots to fractional exponents. You can rewrite any root as an exponent with a fractional value. The pattern is pretty straightforward once you're used to it:[11]
- ...and so on.
-
2Combine the terms using exponent rules. Once you've converted your terms to exponent form, follow the rules of exponents to combine them into a single expression.[12]
- Example: Write as one radical expression.
- Rewrite each term in exponent form: becomes , and becomes .
- The whole expression is now .
- Since the exponents have the same base (3), multiplying them together gives us the same base raised to the sum of the two exponents: .
- Simplify to .
-
3Convert back to radical form. Once you have a single term with a fractional exponent, rewrite it as a radical expression. (The denominator moves to the root, and the numerator stays as an exponent.)[13]
-
4Simplify if possible. If you have any multiplication or exponents left, calculate them so your final answer is in simplest form.
Simplifying Radical Expressions with Variables
-
1Cancel out exponents and roots just as you would with integers. Algebraic problems involve variables like that can represent any number. The rules for exponents and roots still apply to these variables.[14]
- Example: Simplify .
- Combine the terms under the cube root just like you would a number:
- Since the root and the exponent values match, they cancel out to make .
-
2Give positive solutions to even roots. Notice how and both equal 4. That means that 4 (or any positive number) actually has two square roots: one positive number and one negative. But the square root symbol , by default, only refers to the positive number. For instance, you can simplify to , and ignore the negative solution.[15]
- The same is true of any even root: , and so on.
- This does not apply to odd roots like or . The odd root of a negative number is always negative, and the odd root of a positive number is always positive. (Test this yourself by calculating and .)
-
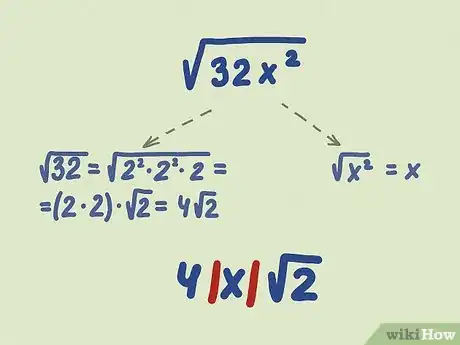
3Use the absolute value symbol to make a variable positive. Variables are tricky: we don't know whether they represent a positive or a negative number. Since the square root (or any even root) function must always give a positive answer, we make sure this happens by using the absolute value symbol around the answers, like this: |x|. This symbol just means "make this value positive."[16]
- Example: Simplify .
- Simplify the non-variable term: .
- Simplify the variable component by canceling out the root and exponent: .
- To make sure the solution to the root is positive, add absolute value symbols around that term: |x|.
- Write the whole expression: 4|x|.
Community Q&A
-
QuestionHow do I simplify radicals?
 Community AnswerYou can only take something out from under a radical if it's a factor. For instance, sqrt(64*(x+3)) can become 8*sqrt(x+3), but sqrt(64x + 3) cannot be simplified.
Community AnswerYou can only take something out from under a radical if it's a factor. For instance, sqrt(64*(x+3)) can become 8*sqrt(x+3), but sqrt(64x + 3) cannot be simplified. -
QuestionA rectangle has sides of 4 and 6 units. On each of its four sides, square are drawn externally. Their centers form another quadrilateral. What is the area (in sq. units) of this quadrilateral?
 DonaganTop AnswererYou'll have to draw a diagram of this. You'll see that triangles can be drawn external to all four sides of the new quadrilateral. By the Pythagorean theorem you can find the sides of the quadrilateral, all of which turn out to be 5 units, so that the quadrilateral's area is 25 square units.
DonaganTop AnswererYou'll have to draw a diagram of this. You'll see that triangles can be drawn external to all four sides of the new quadrilateral. By the Pythagorean theorem you can find the sides of the quadrilateral, all of which turn out to be 5 units, so that the quadrilateral's area is 25 square units. -
QuestionHow do you match a radical expression with the equivalent exponential expression?
 Myles_SchallerCommunity AnswerYou can rewrite any radical expression as a fractional exponent. For example, the square root of 5 is the same as 5 to the power of 1/2. The type of root determines the bottom number of the fraction, so the fourth root of 5 is the same as 5 to the power of 1/4. If there is an exponent already inside the square root, it becomes the top number of the new exponent. So the square root of (3^5) becomes 3 raised to the power of (5/2).
Myles_SchallerCommunity AnswerYou can rewrite any radical expression as a fractional exponent. For example, the square root of 5 is the same as 5 to the power of 1/2. The type of root determines the bottom number of the fraction, so the fourth root of 5 is the same as 5 to the power of 1/4. If there is an exponent already inside the square root, it becomes the top number of the new exponent. So the square root of (3^5) becomes 3 raised to the power of (5/2).
Warnings
- The square root (or any even root) of a negative number can't be simplified without using complex numbers. For now, leave expressions like alone, and treat them as separate from the rest of the expression. (Odd roots like or can handle negative numbers just fine.)[17]⧼thumbs_response⧽
References
- ↑ https://www.mesacc.edu/~scotz47781/mat120/notes/radicals/simplify/simplifying.html
- ↑ https://www.purplemath.com/modules/factnumb.htm
- ↑ https://www.khanacademy.org/math/algebra-2018/rational-exponents-and-radicals/alg1-simplify-square-roots/a/simplifying-square-roots-review
- ↑ https://www.khanacademy.org/math/algebra-2018/rational-exponents-and-radicals/alg1-simplify-square-roots/a/simplifying-square-roots-review
- ↑ https://www.mesacc.edu/~scotz47781/mat120/notes/radicals/simplify/simplifying.html
- ↑ https://mathbitsnotebook.com/Algebra2/Radicals/RDSimplifyingRadicalsCubeRoots.html
- ↑ https://mathbitsnotebook.com/Algebra2/Radicals/RDSimplifyingRadicalsCubeRoots.html
- ↑ https://www.purplemath.com/modules/radicals4.htm
- ↑ https://www.wtamu.edu/academic/anns/mps/math/mathlab/int_algebra/int_alg_tut41_rationalize.htm
- ↑ https://www.wtamu.edu/academic/anns/mps/math/mathlab/int_algebra/int_alg_tut41_rationalize.htm
- ↑ https://www.montereyinstitute.org/courses/DevelopmentalMath/COURSE_TEXT2_RESOURCE/U16_L1_T3_text_final.html
- ↑ https://www.purplemath.com/modules/radicals7.htm
- ↑ https://www.purplemath.com/modules/radicals7.htm
- ↑ https://mathbitsnotebook.com/Algebra2/Radicals/RDSimplifyingRadicalsCubeRoots.html
- ↑ https://www.learnalberta.ca/content/memg/Division03/Principal%20Square%20Root/
- ↑ http://matcmath.org/press/6-1-simplifying-expressions-with-roots-and-fractional-exponents/
- ↑ http://matcmath.org/press/6-1-simplifying-expressions-with-roots-and-fractional-exponents/
About This Article
To simplify a radical expression, simplify any perfect squares or cubes, fractional exponents, or negative exponents, and combine any like terms that result. If there are fractions in the expression, split them into the square root of the numerator and square root of the denominator. If you need to extract square factors, factorize the imperfect radical expression into its prime factors and remove any multiples that are a perfect square out of the radical sign. For tips on rationalizing denominators, read on!




![{\displaystyle {\sqrt[{3}]{}}}](./images/2033065958-8e7fcb4f3c42dd8748d4012549cc9deb29615a2f.webp)
![{\displaystyle {\sqrt[{4}]{}}}](./images/1989943279-ef063fe7a70b659e20ec34700cbc12ab2e4511eb.webp)













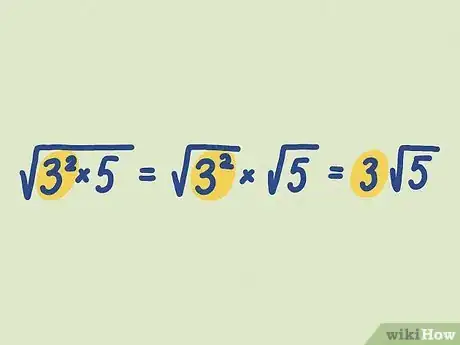










![{\displaystyle {\sqrt[{3}]{81}}}](./images/2336366764-ca9febe699fd355cf5b26c8e19fa9a2c6164b7da.webp)

![{\displaystyle {\sqrt[{3}]{81}}={\sqrt[{3}]{3\times 3\times 3\times 3}}}](./images/2243043518-95cbc45d961ad7cc0640bdbabffe5bf2bfc26361.webp)
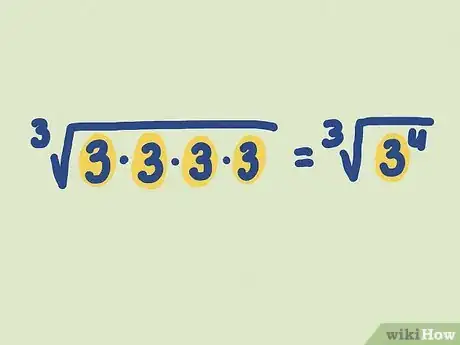
![{\displaystyle {\sqrt[{3}]{3\times 3\times 3\times 3}}={\sqrt[{3}]{3^{4}}}}](./images/1785143067-fd9b8677c52a5a3746109e140ad7869af30332e0.webp)
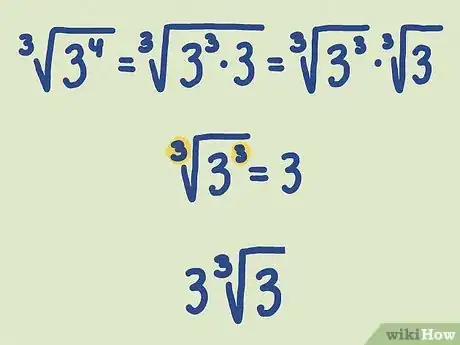
![{\displaystyle {\sqrt[{3}]{3^{4}}}={\sqrt[{3}]{3^{3}\times 3}}={\sqrt[{3}]{3^{3}}}{\sqrt[{3}]{3}}}](./images/1726095235-09d12742a3235af1dd6b244f15a4dacad501720b.webp)
![{\displaystyle {\sqrt[{3}]{3^{3}}}}](./images/1820073943-25e91a6741ef10654cb0c5daa81c38fe08ce7a87.webp)

![{\displaystyle 3{\sqrt[{3}]{3}}}](./images/2013142940-2e6a558ebf34dae326f1803dba31c6be66440911.webp)
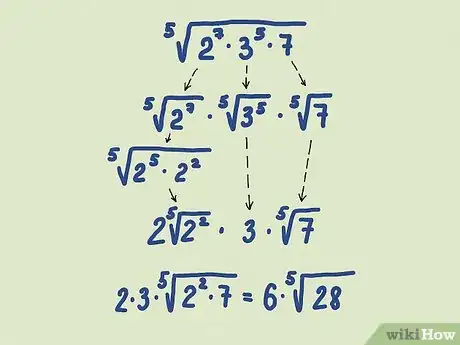
![{\displaystyle {\sqrt[{5}]{2^{7}\times 3^{5}\times 7}}}](./images/1756307286-dc6498620d0486bb70a3fd7327884bcfe15d7284.webp)
![{\displaystyle {\sqrt[{5}]{2^{7}}}{\sqrt[{5}]{3^{5}}}{\sqrt[{5}]{7}}}](./images/1852055450-91f29c2b5a6a945b63a63a8a2f4d06e23b4a44d0.webp)
![{\displaystyle {\sqrt[{5}]{2^{7}}}={\sqrt[{5}]{2^{5}\times 2^{2}}}}](./images/1839210381-5b93c6df23cc07d02753d027ff95863488fc7e6b.webp)
![{\displaystyle 2{\sqrt[{5}]{2^{2}}}}](./images/2087264371-a15717d47e8c1cbeaa7dcb597c4c82f5f5b948ca.webp)
![{\displaystyle {\sqrt[{5}]{3^{5}}}}](./images/1839865723-bd247559c0d61cc4bd611920cad06968e981f82a.webp)
![{\displaystyle {\sqrt[{5}]{7}}}](./images/1942757351-b1b516a488d6f61ebb58c63c2d48f5943afcb786.webp)
![{\displaystyle 2{\sqrt[{5}]{2^{2}}}\times 3\times {\sqrt[{5}]{7}}}](./images/1891377119-a555d94dc0bf37890412d2674fdecdd24e2c9c54.webp)
![{\displaystyle (2\times 3){\sqrt[{5}]{2^{2}\times 7}}}](./images/1871126393-247ae24c7ae63a85a717e594faca880133d7c191.webp)
![{\displaystyle 6{\sqrt[{5}]{28}}}](./images/2037719057-7a77a9ddd6435b36d4a698fd24fdab3fb35045c5.webp)














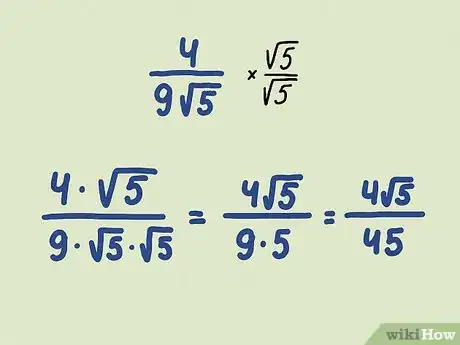



![{\displaystyle {\sqrt[{3}]{x}}=x^{\frac {1}{3}}}](./images/2093293621-e9ce837de6bd19e3408d760c739df89edce67a99.webp)
![{\displaystyle {\sqrt[{4}]{x}}=x^{\frac {1}{4}}}](./images/1924276142-7a12ce88946ba6ee267c1a9079aad6cf704533e1.webp)
![{\displaystyle {\sqrt {3}}{\sqrt[{4}]{3}}}](./images/1704665027-3f0c1899289c23a81944d8d09f9ac5ed39fe25dc.webp)

![{\displaystyle {\sqrt[{4}]{3}}}](./images/2329419933-a3dbdc22c431f9de5b94f2dd7afbdc9e9c423736.webp)




![{\displaystyle 3^{\frac {3}{4}}={\sqrt[{4}]{3^{3}}}}](./images/1916149608-010cdd6dcd3d20f84c017771d961d4b62f63c340.webp)
![{\displaystyle {\sqrt[{4}]{3^{3}}}={\sqrt[{4}]{9}}}](./images/2036670630-024a66e89fad68dc89da95b82ed94ab1b2beae7d.webp)
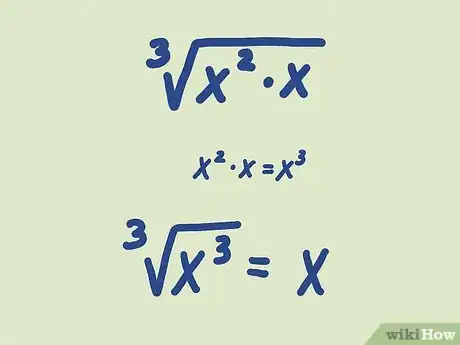

![{\displaystyle {\sqrt[{3}]{x^{2}\times x}}}](./images/1918377811-4e9dda61f61b9767c52e152b3e8f567b2d224661.webp)
![{\displaystyle {\sqrt[{3}]{x^{3}}}}](./images/2350850292-b5d6a326caddab6a5d0a9cb65dd557cecc7a76c8.webp)
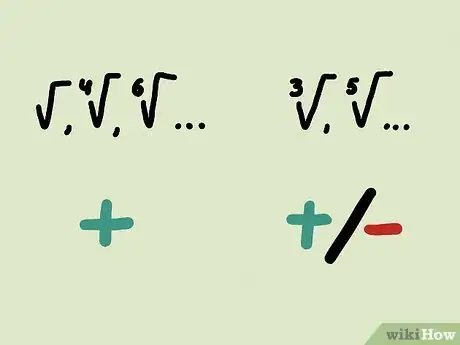





![{\displaystyle {\sqrt {}},{\sqrt[{4}]{}},{\sqrt[{6}]{}}}](./images/2122653839-9946f87efba8452f37fddd6d8dc6ecf4d70c6c93.webp)
![{\displaystyle {\sqrt[{5}]{}}}](./images/1833115508-8e97a324789cb01dd50fb8d2a3c41c34a487060e.webp)