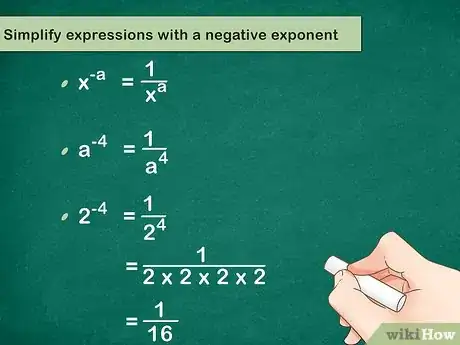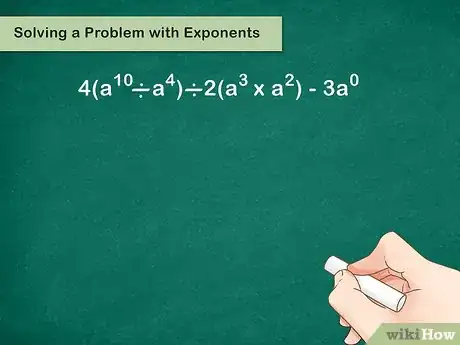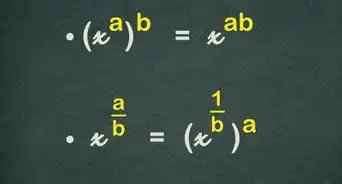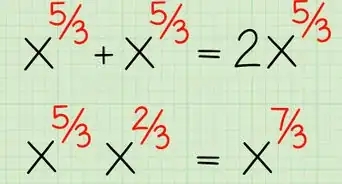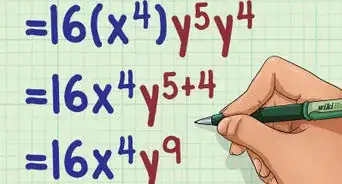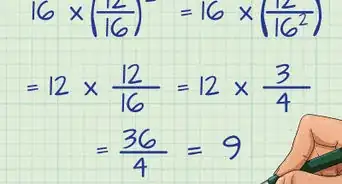How to Solve Algebraic Problems With Exponents

Co-authored by David Jia

Last Updated: March 3, 2023 References

In algebra, the operations (adding, subtracting, multiplying, and dividing) performed on variables work the same as the operations performed on numbers. When performing these operations on exponents, however, the laws are different. By learning these special rules for exponents, you can easily simplify algebraic expressions that include them.

Part 1

Part 1 of 2:

Understanding the Laws of Exponents

1
Solve expressions with a positive exponent. An exponent simply tells you how many times you multiply the base (big number) by itself.^{[1]
X
Research source}
- For example, $x^{3}$ is the same as $x\times x\times x$ .
- Plugging in a number, you would have
  $2^{3}$
  = $2\times 2\times 2$
  = $8$
- Expressions to the first degree (expressions with an exponent of 1) always simplify to the base. It is like saying “x one time.” For example, $x^{1}=x$ .
- Expressions to the zero degree (expressions with an exponent of 0) always simplify to 1. For example, $x^{0}=1$ .
2
Simplify multiplication expressions with a positive exponent. When you multiply two exponents with the same base, you can simplify the expression by adding the exponents. Do NOT add or multiply the base.^{[2]
X
Research source}
- This rule does not apply to numbers that have a different base. For example, you cannot simplify $2^{3}\times 3^{2}$ , you simply have to solve the exponents separately and then multiply the two numbers.
- For example, $x^{2}\times x^{4}$ is the same as $x^{2+4}$ , which is the same as $x^{6}$ .
- Plugging in a number, you would have
  $2^{2}\times 2^{4}$
  = $2^{2+4}$
  = $2^{6}$
  = $2\times 2\times 2\times 2\times 2\times 2$
  = $64$
Advertisement
3
Simplify division expressions with a positive exponent. When you divide to exponents with the same base, you can simplify the expression by subtracting the exponents.^{[3]
X
Research source} Do NOT divide or subtract the base.
- For example, ${\frac {x^{10}}{x^{5}}}$ is the same as $x^{10-5}$ , which is the same as $x^{5}$ .
- Plugging in a number, you would have
  ${\frac {2^{10}}{2^{5}}}$
  = $2^{10-5}$
  = $2^{5}$
  = $2\times 2\times 2\times 2\times 2$
  = $32$
4
Simplify exponents with a positive exponent. Sometimes an exponent will have an exponent. In this situation, you would multiply the two exponents.^{[4]
X
Research source}
- For example, $(x^{2})^{3}$ is the same as $x^{2\times 3}$ , which is the same as $x^{6}$ .
- Plugging in a number, you would have
  $(2^{2})^{3}$
  = $2^{2\times 3}$
  = $2^{6}$
  = $2\times 2\times 2\times 2\times 2\times 2$
  = $64$
5
Simplify expressions with a negative exponent. You can think of a negative exponent as being the opposite of a positive exponent. Since a positive exponent tells you how many times to multiply, a negative exponent tells you how many times to divide.^{[5]
X
Research source} To simplify an expression with a negative exponent, use the formula $x^{-a}={\frac {1}{x^{a}}}$ $x^{{-a}}={\frac {1}{x^{{a}}}}$ .
- For example, $x^{-4}$ is the same as ${\frac {1}{x^{4}}}$ .
- Plugging in a number,
  $2^{-4}$
  = ${\frac {1}{2^{4}}}$
  = ${\frac {1}{2\times 2\times 2\times 2}}$
  = ${\frac {1}{16}}$

Part 2

Part 2 of 2:

Solving a Problem with Exponents

1
Address the order of operations. Just like any problem in mathematics, an algebraic problem must be completed by the order of operations. You can use the phrase "Please Excuse My Dear Aunt Sally," or the acronym PEMDAS, to help you remember Parentheses, Exponents, Multiplication, Division, Addition, Subtraction.^{[6]
X
Research source}
- For example, if the problem is $4(x^{10}\div x^{4})\div 2(x^{3}\times x^{2})-3x^{0}$ , you would first complete the calculations inside the parentheses.
2
Simplify the expressions using the laws of exponents. Remember, you can only simplify if the exponents have the same base.^{[7]
X
Research source}
- For example, $x^{10}\div x^{4}$ can simplify to $x^{10-4}$ , or $x^{6}$ .
  $x^{3}\times x^{2}$ can simplify to $x^{3+2}$ , or $x^{5}$ .
  $x^{0}$ is 1, since any number to the zero power is 1.
  So, the simplified problem becomes $4(x^{6})\div 2(x^{5})-3(1)$ .
3
Simplify coefficients. Coefficients are the numbers in an algebraic problem. When simplifying coefficients with exponents, you complete the regular operations.^{[8]
X
Research source}
- For example, for $4(x^{6})\div 2(x^{5})$ , you would first divide the coefficients:
  $4\div 2=2$ .
  Then, divide the exponents:
  $x^{6}\div x^{5}$
  = $x^{6-5}$
  = $x^{1}$
  = $x$ .
  Since $3(1)$ simplifies to $3$ , the final, simplified problem is $2x-3$ .

Community Q&A

Question

How can I solve an unknown exponent, e.g 2^y?

Donagan

Top Answerer

The expression would have to be part of an equation before you could find the value of y.
Question

How do I simplify algebraic expressions?

Donagan

Top Answerer

See Simplify Algebraic Expressions.
Question

How do I answer if the problem is in sentence form?

Community Answer

Do your best to take key vocabulary and transform it into math, then take it from there.