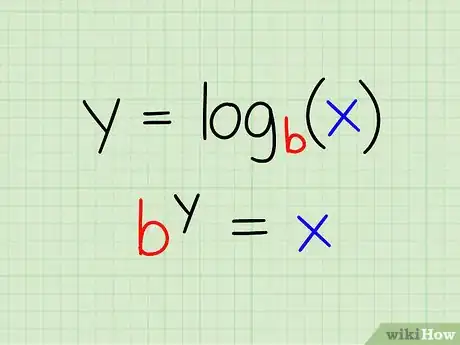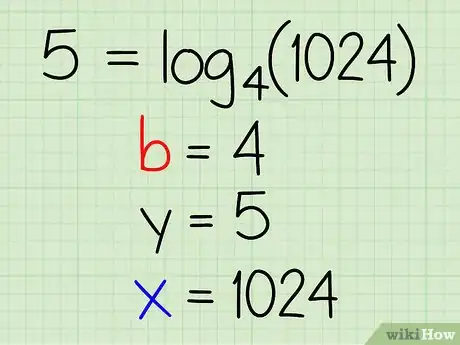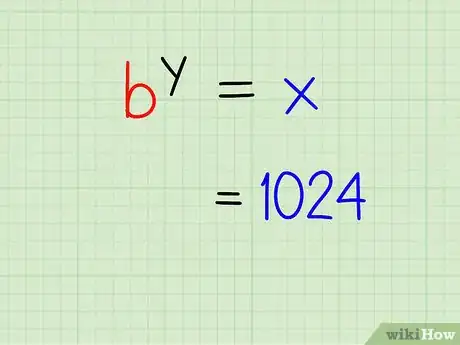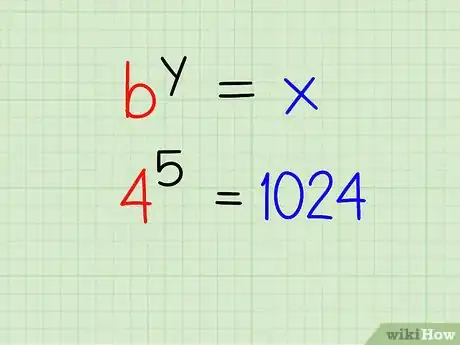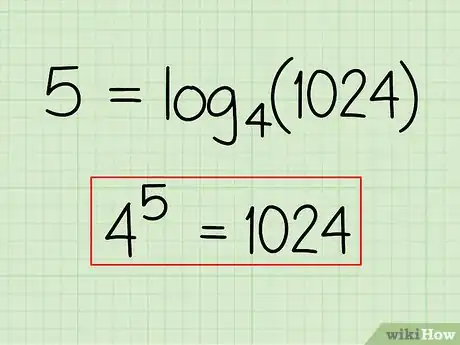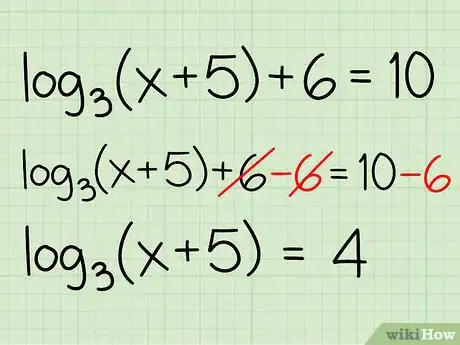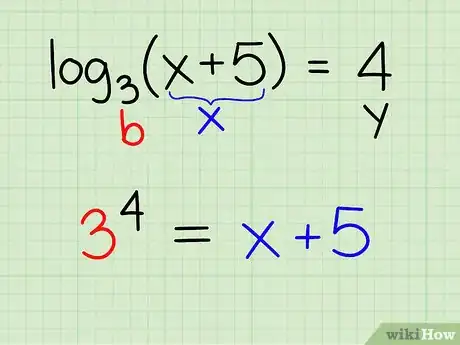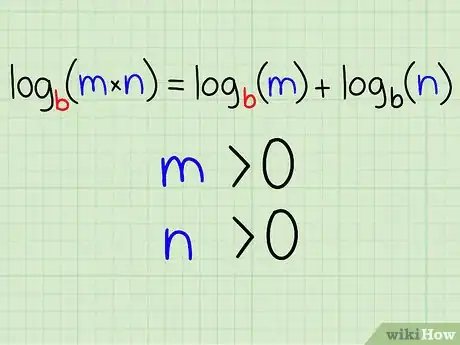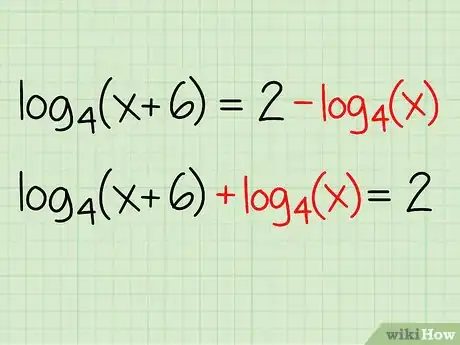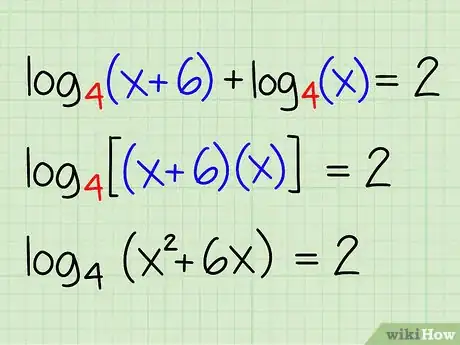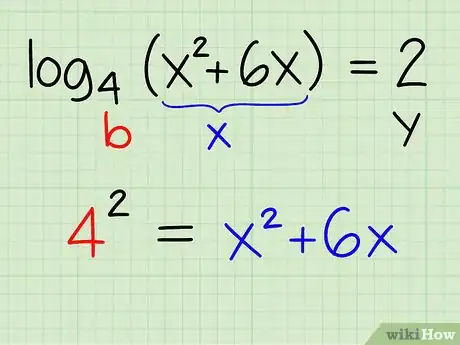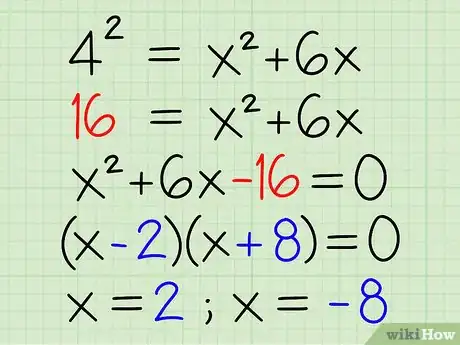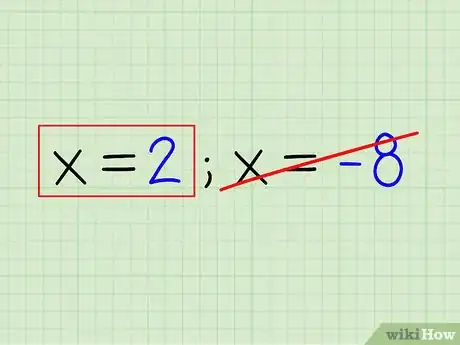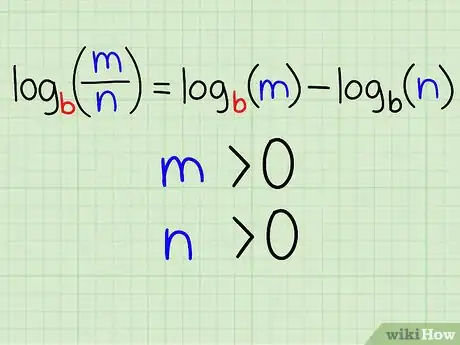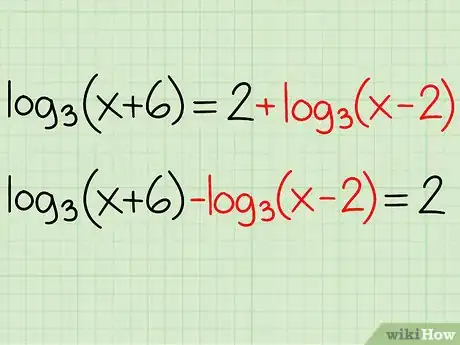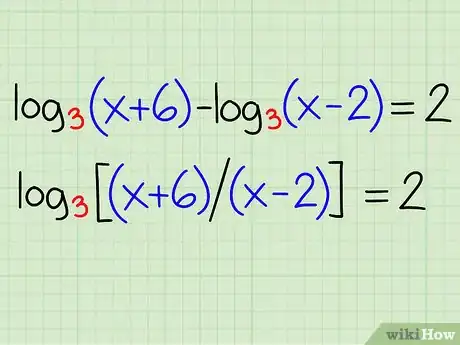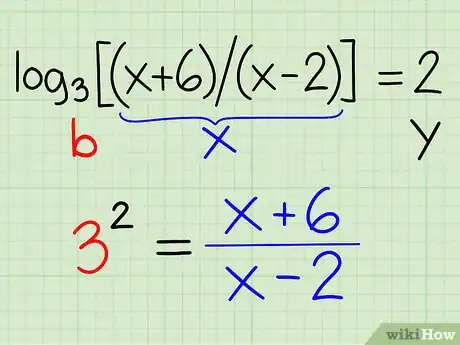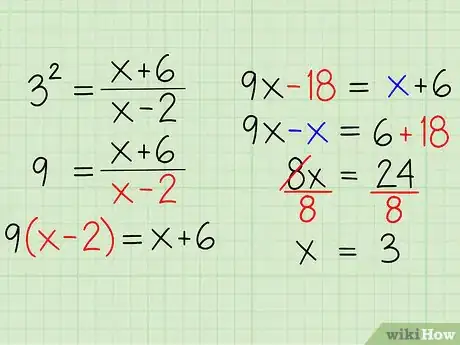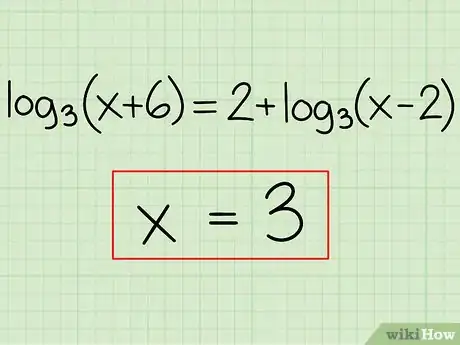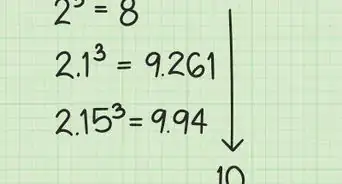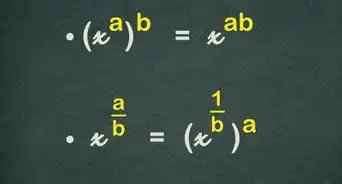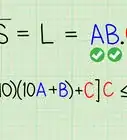How to Solve Logarithms

Logarithms might be intimidating, but solving a logarithm is much simpler once you realize that logarithms are just another way to write out exponential equations. Once you rewrite the logarithm into a more familiar form, you should be able to solve it as you would solve any standard exponential equation.

Steps

Before You Begin: Learn to Express a Logarithmic Equation Exponentially[1] [2]

  1. Image titled Solve Logarithms Step 1
    1
    Know the logarithm definition. Before you can solve logarithms, you need to understand that a logarithm is essentially another way to write an exponential equation. It's precise definition is as follows:
    • y = logb (x)
      • If and only if: by = x
    • Note that b is the base of the logarithm. It must also be true that:
      • b > 0
      • b does not equal 1
    • In the same equation, y is the exponent and x is the exponential expression that the logarithm is set equal to.
  2. Image titled Solve Logarithms Step 2
    2
    Look at the equation. When looking at the problem equation, identify the base (b), exponent (y), and exponential expression (x).
    • Example: 5 = log4(1024)
      • b = 4
      • y = 5
      • x = 1024
    Advertisement
  3. Image titled Solve Logarithms Step 3
    3
    Move the exponential expression to one side of the equation. Set the value of your exponential expression, x, to one side of the equal sign.
    • Example: 1024 = ?
  4. Image titled Solve Logarithms Step 4
    4
    Apply the exponent to the base. The value of your base, b, needs to be multiplied by itself by the amount of times indicated by your exponent, y.
    • Example: 4 * 4 * 4 * 4 * 4 = ?
      • This could also be written as: 45
  5. Image titled Solve Logarithms Step 5
    5
    Rewrite your final answer. You should be able to rewrite the logarithm as an exponential expression now. Verify that your answer is correct by making sure that both sides of the equation are equal.
    • Example: 45 = 1024
    6. Advertisement
Method 1
Method 1 of 3:

Method One: Solve for X

  1. Image titled Solve Logarithms Step 6
    1
    Isolate the logarithm. Use inverse operations to move any part of the equation that is not part of the logarithm to the opposite side of the equation.
    • Example: log3(x + 5) + 6 = 10
      • log3(x + 5) + 6 - 6 = 10 - 6
      • log3(x + 5) = 4
  2. Image titled Solve Logarithms Step 7
    2
    Rewrite the equation in exponential form. Using what you now know about the relationship between logarithms and exponential equations, break the logarithm apart and rewrite the equation in a simpler, solvable exponential form.
    • Example:log3(x + 5) = 4
      • Comparing this equation to the definition [y = logb (x)], you can conclude that: y = 4; b = 3; x = x + 5
      • Rewrite the equation so that: by = x
      • 34 = x + 5
  3. Image titled Solve Logarithms Step 8
    3
    Solve for x. With the problem simplified into a basic exponential equation, you should be able to solve it as you would solve any exponential equation.
    • Example: 34 = x + 5
      • 3 * 3 * 3 * 3 = x + 5
      • 81 = x + 5
      • 81 - 5 = x + 5 - 5
      • 76 = x
  4. Image titled Solve Logarithms Step 9
    4
    Write your final answer. The answer you got when solving for x is the solution to your original logarithm.
    • Example: x = 76
    5. Advertisement
Method 2
Method 2 of 3:

Method Two: Solve for X Using the Logarithmic Product Rule[3] [4]

  1. Image titled Solve Logarithms Step 10
    1
    Know the product rule. The first property of logarithms, known as the "product rule," states that the logarithm of a multiplied product equals the sum of the logarithms of both factors. Written in equation form:
    • logb(m * n) = logb(m) + logb(n)
    • Also note that the following must be true:
      • m > 0
      • n > 0
  2. Image titled Solve Logarithms Step 11
    2
    Isolate the logarithm to one side of the equation. Use inverse operations to shift the parts of the equation around so that all logarithms are on one side of the equation while all other elements are on the opposite side.
    • Example: log4(x + 6) = 2 - log4(x)
      • log4(x + 6) + log4(x) = 2 - log4(x) + log4(x)
      • log4(x + 6) + log4(x) = 2
  3. Image titled Solve Logarithms Step 12
    3
    Apply the product rule. If there are two logarithms added together in the equation, you can use the product rule to combine the two logarithms into one.
    • Example: log4(x + 6) + log4(x) = 2
      • log4[(x + 6) * x] = 2
      • log4(x2 + 6x) = 2
  4. Image titled Solve Logarithms Step 13
    4
    Rewrite the equation in exponential form. Remember that a logarithm is just another way to write an exponential equation. Use the logarithm definition to rewrite the equation in its solvable form.
    • Example: log4(x2 + 6x) = 2
      • Comparing this equation to the definition [y = logb (x)], you can conclude that: y = 2; b = 4 ; x = x2 + 6x
      • Rewrite the equation so that: by = x
      • 42 = x2 + 6x
  5. Image titled Solve Logarithms Step 14
    5
    Solve for x. Now that the equation has become a standard exponential equation, use your knowledge of exponential equations to solve for x as you usually would.
    • Example: 42 = x2 + 6x
      • 4 * 4 = x2 + 6x
      • 16 = x2 + 6x
      • 16 - 16 = x2 + 6x - 16
      • 0 = x2 + 6x - 16
      • 0 = (x - 2) * (x + 8)
      • x = 2; x = -8
  6. Image titled Solve Logarithms Step 15
    6
    Write your answer. At this point, you should have the solution for the equation. Write it down in the space provided for your answer.
    • Example: x = 2
    • Note that you cannot have a negative solution for a logarithm, so you can discard x - 8 as a solution.
    7. Advertisement
Method 3
Method 3 of 3:

Method Three: Solve for X Using the Logarithmic Quotient Rule[5]

  1. Image titled Solve Logarithms Step 16
    1
    Know the quotient rule. According to the second property of logarithms, known as the "quotient rule," the logarithm of a quotient can be rewritten by subtracting the logarithm of the denominator from the logarithm of the numerator. Written as an equation:
    • logb(m / n) = logb(m) - logb(n)
    • Also note that the following must be true:
      • m > 0
      • n > 0
  2. Image titled Solve Logarithms Step 17
    2
    Isolate the logarithm to one side of the equation. Before you can solve the logarithm, you need to shift all logs in the equation to one side of the equal sign. The other parts of the equation should all be shifted to the opposite side of the equation. Use inverse operations to accomplish this.
    • Example: log3(x + 6) = 2 + log3(x - 2)
      • log3(x + 6) - log3(x - 2) = 2 + log3(x - 2) - log3(x - 2)
      • log3(x + 6) - log3(x - 2) = 2
  3. Image titled Solve Logarithms Step 18
    3
    Apply the quotient rule. If there are two logarithms in the equation and one must be subtracted by the other, you can and should use the quotient rule to combine the two logarithms into one.
    • Example: log3(x + 6) - log3(x - 2) = 2
      • log3[(x + 6) / (x - 2)] = 2
  4. Image titled Solve Logarithms Step 19
    4
    Rewrite the equation in exponential form. Now that there is only one logarithm in the equation, use the logarithms definition to rewrite the equation in exponential form, thereby removing the log.
    • Example: log3[(x + 6) / (x - 2)] = 2
      • Comparing this equation to the definition [y = logb (x)], you can conclude that: y = 2; b = 3; x = (x + 6) / (x - 2)
      • Rewrite the equation so that: by = x
      • 32 = (x + 6) / (x - 2)
  5. Image titled Solve Logarithms Step 20
    5
    Solve for x. With the equation now in exponential form, you should be able to solve for x as you usually would.
    • Example: 32 = (x + 6) / (x - 2)
      • 3 * 3 = (x + 6) / (x - 2)
      • 9 = (x + 6) / (x - 2)
      • 9 * (x - 2) = [(x + 6) / (x - 2)] * (x - 2)
      • 9x - 18 = x + 6
      • 9x - x - 18 + 18 = x - x + 6 + 18
      • 8x = 24
      • 8x / 8 = 24 / 8
      • x = 3
  6. Image titled Solve Logarithms Step 21
    6
    Write your final answer. Go back and double-check your steps. Once you feel certain that you have the correct solution, write it down.
    • Example: x = 3
    7. Advertisement

Community Q&A

  • Question
    Why do we consider positive answers only?
    Community Answer
    Community Answer
    Logarithmic graphs have asymptotes at x=0, therefore any negative answers cannot exist.
  • Question
    How do I find the antilog of 12.18?
    Linnie
    Linnie
    Top Answerer
    Understand that the antilog of 12.18 is a common antilogarithm question, which means the assumed subscript is 10. To solve this problem, take 10 to the power of 12.18. This gives you an approximate value of 1,513,561,248,436.21.
  • Question
    How do you do 4^x+10 = 10?
    Community Answer
    Community Answer
    4^x + 10 = 10. Subtract 10 from both sides. 4^x = 0. Rewrite according to the definition of a logarithm. log4(0) = x. Use the change of base formula to calculate log4(0). log(0)/log(4) = x log(0) is undefined, making x undefined as well.
Advertisement

You Might Also Like

Calculate a Square Root by Hand
How to
Calculate a Square Root by Hand
Simplify a Square Root
How to
Simplify a Square Root
Find a Square Root Without a Calculator
How to
Find a Square Root Without a Calculator
Calculate Cube Root by Hand
How to
Calculate Cube Root by Hand
Read a Logarithmic Scale
How to
Read a Logarithmic Scale
Solve Decimal Exponents
How to
Solve Decimal Exponents
Add Exponents
How to
Add Exponents
Use Logarithmic Tables
How to
Use Logarithmic Tables
Multiply Exponents
How to
Multiply Exponents
Solve Exponents
How to
Solve Exponents
Square Fractions
How to
Square Fractions
Do Antilog
How to
Do Antilog
Calculate Negative Exponents
How to
Calculate Negative Exponents
Divide Logarithms
How to
Divide Logarithms
Advertisement

References

  1. ↑ https://www.wtamu.edu/academic/anns/mps/math/mathlab/col_algebra/col_alg_tut43_logfun.htm#logdef
  2. ↑ https://www.mathsisfun.com/algebra/logarithms.html
  3. ↑ https://www.wtamu.edu/academic/anns/mps/math/mathlab/col_algebra/col_alg_tut46_logeq.htm
  4. ↑ https://www.youtube.com/watch?v=fnhFneOz6n8
  5. ↑ https://www.wtamu.edu/academic/anns/mps/math/mathlab/col_algebra/col_alg_tut44_logprop.htm

About This Article

wikiHow is a “wiki,” similar to Wikipedia, which means that many of our articles are co-written by multiple authors. To create this article, volunteer authors worked to edit and improve it over time. This article has been viewed 188,099 times.
101 votes - 72%
Co-authors: 3
Updated: March 10, 2023
Views: 188,099
Categories: Exponents and Logarithms
Article SummaryX

To solve a logarithm, start by identifying the base, which is "b" in the equation, the exponent, which is "y," and the exponential expression, which is "x." Then, move the exponential expression to one side of the equation, and apply the exponent to the base by multiplying the base by itself the number of times indicated in the exponent. Finally, rewrite your final answer as an exponential expression. To learn how to solve for "x" in a logarithm, scroll down!

Did this summary help you?
Advertisement