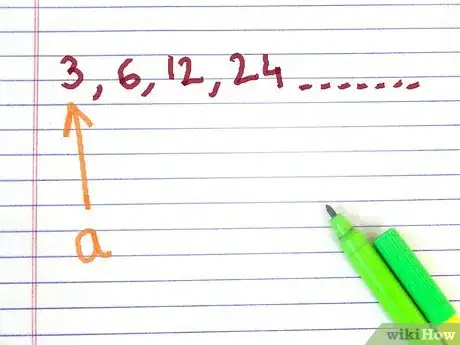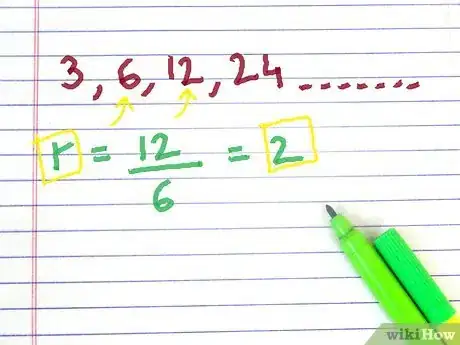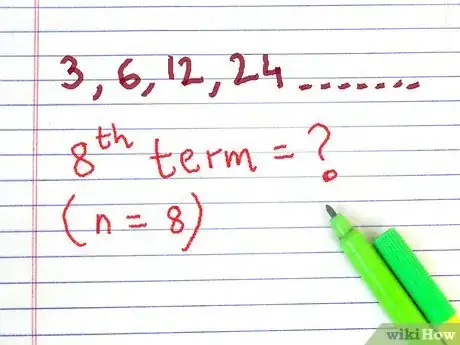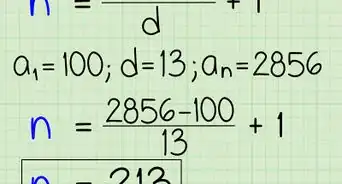X
wikiHow is a “wiki,” similar to Wikipedia, which means that many of our articles are co-written by multiple authors. To create this article, 13 people, some anonymous, worked to edit and improve it over time.
This article has been viewed 210,738 times.
Learn more...
A geometric sequence is a sequence derived by multiplying the last term by a constant.[1] Geometric progressions have many uses in today's society, such as calculating interest on money in a bank account. So if you were wondering how exactly you would work out how much money you'll have in there in a few years, this article will help you find out.
Steps
-
1Identify the first term in the sequence, call this number a.[2]
-
2Calculate the common ratio (r) of the sequence. It can be calculated by dividing any term of the geometric sequence by the term preceding it.[3]Advertisement
-
3Identify the number of term you wish to find in the sequence. Call this number n.[4]
- For example, if you wish to find the 8th term in the sequence, then n = 8.
-
4The nth term is given by arn-1. Simply insert the values of a, r and n in this formula and evaluate the resulting expression to get the nth term.[5]
Advertisement
Community Q&A
-
QuestionHow do I find the nth term in the sequence 1, 2, 4, 7, 11?
 DonaganTop AnswererYou can't do it, because that is neither a geometric nor an arithmetic sequence.
DonaganTop AnswererYou can't do it, because that is neither a geometric nor an arithmetic sequence. -
QuestionHow do I get the first term in a geometric sequence?
 Community AnswerTake this for example. If you have given a3 = 27 and r = 3, divide 27 by 3, which is 9. Divide again by 3 and get 3. Then you have a1 = 3, a2 = 9, and a3 = 27. If you know the constant and one term in the geometric sequence, you can calculate any other term in the sequence.
Community AnswerTake this for example. If you have given a3 = 27 and r = 3, divide 27 by 3, which is 9. Divide again by 3 and get 3. Then you have a1 = 3, a2 = 9, and a3 = 27. If you know the constant and one term in the geometric sequence, you can calculate any other term in the sequence. -
QuestionHow do I get the nth term in a geometric sequence if the first term isn't given?
 DonaganTop AnswererIf you are given any term in the sequence, treat it as if it's the first term, and proceed as usual from there. If you're not given any terms in the sequence, you cannot find the nth term.
DonaganTop AnswererIf you are given any term in the sequence, treat it as if it's the first term, and proceed as usual from there. If you're not given any terms in the sequence, you cannot find the nth term.
Advertisement
References
- ↑ https://www.mathsisfun.com/algebra/sequences-sums-geometric.html
- ↑ http://mathematics.laerd.com/maths/geometric-progression-intro.php
- ↑ https://www.khanacademy.org/math/algebra/x2f8bb11595b61c86:sequences/x2f8bb11595b61c86:constructing-geometric-sequences/a/geometric-sequences-review
- ↑ https://www.cuemath.com/algebra/geometric-sequence/
- ↑ https://mathbitsnotebook.com/Algebra2/Sequences/SSGeometric.html
About This Article
Advertisement