This article was co-authored by wikiHow Staff. Our trained team of editors and researchers validate articles for accuracy and comprehensiveness. wikiHow's Content Management Team carefully monitors the work from our editorial staff to ensure that each article is backed by trusted research and meets our high quality standards.
There are 10 references cited in this article, which can be found at the bottom of the page.
This article has been viewed 65,173 times.
Learn more...
If you used the same unit to weigh molecules and elephants, your measurements would end up really complicated. The international system of units, called SI units, solves this problem by using prefixes. Each prefix multiplies the base unit by a certain power of ten (10, 100, 1000, and so on). This keeps the numbers you're working with manageable, while quickly identifying the relationship between very large and very small units. All SI units use the same prefixes, so once you learn them for units of length (metres), you already know how to use prefixes for units of mass (grams),
Steps
Learning Basic Conversion
-
1Learn the definition of "kilo." "Kilo" is one of the most common unit prefixes, so you might already recognize it from words like "kilogram" and "kilometre". This prefix means "1000" (one thousand). Kilo- is abbreviated as "k-", so a kilogram is "kg" and a kilometre is "km".[1]
-
2Convert kilometres to metres. Since kilo- means 1 000, one kilometre (km) is equal to 1000 metres (m). Multiply the number of kilometres by 1 000 to get the same measurement in metres.[2]
- For example, 75 kilometres = = 75 000 metres.
- To make sure you've set up the conversion correctly, try reading it in plain English: means "1 000 metres per kilometre".
Advertisement -
3Compare to other units. The base unit does not make any difference in this calculation. As long as you know the definition of the prefix, you can use the same math to convert between it and the base unit. Here are a couple examples:
-
4Learn common larger prefixes. Another common prefix is mega-, which means one million (1 000 000) and is abbreviated M. Even larger units use the prefix giga-, which means one billion (1 000 000 000) and is abbreviated G.[5] Here are a couple conversions that use these prefixes:
- A 3 megawatt (MW) factory produces = 3 000 000 watts (W) of power.
- A 2 gigajoule (GJ) explosion releases = 2 000 000 000 joules (J) of energy.
-
5Convert from a base unit to a larger unit. To convert to a larger unit of measurement, you'll divide by the conversion factor instead of multiplying. As always, you're less likely to make a mistake if you include the units at each point in your calculation:[6]
- 65 300 metres is equal to = 65.3 kilometres.
-
6Learn prefixes with factors less than one. What if you want to measure a length shorter than one meter, or the volume of a cup smaller than one litre? That's when you use prefixes that represent a fraction of the base unit. Here are the most common prefixes of this type:[7]
- centi- (c) means "one hundredth" (0.01). 1 centimetre = 0.01 metres.
- milli- (m) means "one thousandth" (0.001). 1 millimetre = 0.001 metres.
- micro- (µ) means "one millionth" (0.000 001). 1 micrometre = 0.000 001 metres.
- nano- (n) means "one billionth" (0.000 000 001). 1 nanometre = 0.000 000 001 metres.
-
7Convert between the base unit and smaller units. These conversions work exactly the same. Just make sure to set up your units so they cancel out, and to keep track of decimals:[8]
- Centimetres to metres: 33 centimetres = = 0.33 metres.
- Metres to millimetres: 2.15 metres = = 2150 millimetres.
-
8Check your answer. Probably the most common mistake with these conversions is to accidentally divide instead of multiply or vice versa. There are several ways to catch this mistake:
- Check the units in your equation. If you set it up correctly, the original units should cancel out. For example gives you an answer in terms of . The km units are on top and bottom, so they cancel out and leave you with m (metres).
- Compare the units logically. The smaller unit should always have the larger number next to it. Metres are smaller than kilometres, so it takes more of them to fill the same length. For example, a result of 75 000 metres = 75 kilometres makes sense, since a larger number of metres equals a smaller number of kilometres.
Using Powers of Ten
-
1Learn the prefixes as powers of ten. Every SI prefix represents a different power of ten: 100, 1000, 0.001, and so on. Here are the most common examples written in scientific notation (standard form):[9]
- giga- = 1 000 000 000 = 109
- mega- = 1 000 000 = 106
- kilo- = 1 000 = 103
- centi- = 0.01 = 10-2
- milli- = 0.001 = 10-3
- micro- = 0.000 001 = 10-6
- nano- = 0.000 000 001 = 10-9
- You can also write a negative exponent as a fraction with a positive exponent in the denominator:
-
2Use scientific notation to convert to the base unit. Scientific notation makes it much easier to convert between units of very different size. No matter what the final unit you want is, you can start by converting the initial value to the base unit, using scientific notation.
- Example: How many centimetres are in 13.78 kilometres?
The answer isn't obvious, but you do know that the kilometre is equal to 103 metres.
Therefore, 13.78 km = 13.78 * 103 metres. You'll use this in the next step.
- Example: How many centimetres are in 13.78 kilometres?
-
3Find the conversion to your final unit. Now that you have a base unit value (with no prefix), you can set up an ordinary conversion to the final unit. Write the conversion in powers of ten notation.
- To continue the example, you now want to convert 13.78 * 103 metres into centimetres.
The prefix centi- means 10-2, so there is
- To continue the example, you now want to convert 13.78 * 103 metres into centimetres.
-
4Set up the conversion as a single expression. Set up your conversion using power of ten notation for all values. This gives you a fraction that divides one power of ten by another:
- cm
-
5Simplify the exponents. To divide one exponential expression by the other (when they both have the same base), take the top exponent and subtract the bottom exponent. The answer is the new exponent in your answer, with the same base (which is always 10 in these conversion problems).[10]
- cm = centimeters.
- It's usually helpful to write your answer in scientific notation (standard form): centimeters.
-
6Simplify the formula. Once you are comfortable with this process, you can combine the whole process into a couple quick steps:[11]
- Write the initial prefix and the final prefix as powers of 10. For base units without prefixes, use .
- Divide the initial power of 10 by the final power of 10. (To do this, subtract the final exponent from the initial exponent.)
- Multiply your initial value by this answer.Example: How many centilitres (cL) are in 85 500 millilitres (mL)?
The initial prefix is "milli-" = and the final prefix is "centi-" = .
85 500 millilitres = centilitres.
Optionally, write this in scientific notation: centilitres.
Community Q&A
-
QuestionWhat's the speed of a car in kph if it travels 16 km in 13 minutes?
 DonaganTop AnswererDivide 60 minutes by 13 minutes. That's 4.615. Multiply that by 16 km: (4.615)(16 km) = 73.84 km. That means that if a car travels 16 km in 13 minutes, at the same speed it would travel 73.84 km in one hour. The car is traveling at 73.84 kph.
DonaganTop AnswererDivide 60 minutes by 13 minutes. That's 4.615. Multiply that by 16 km: (4.615)(16 km) = 73.84 km. That means that if a car travels 16 km in 13 minutes, at the same speed it would travel 73.84 km in one hour. The car is traveling at 73.84 kph.
Reference Guide
Complete List of Prefixes
The bold rows represent the most common prefixes.
- yotta | 1024 | Y | 1,000,000,000,000,000,000,000,000 base units
- zetta | 1021 | Z | 1,000,000,000,000,000,000,000
- exa | 1018 | E | 1,000,000,000,000,000,000
- peta | 1015 | P | 1,000,000,000,000,000
- tera | 1012 | T | 1,000,000,000,000
- giga | 109 | G | 1,000,000,000
- mega | 106 | M | 1,000,000
- kilo | 103 | k | 1,000
- hecto | 102 | h | 100
- deka | 101 | da | 10
- (no prefix) | 100 | | 1 base unit
- deci | 10-1 | d | 0.1
- centi | 10-2 | c | 0.01
- milli | 10-3 | m | 0.001
- micro | 10-6 | µ | 0.000001
- nano | 10-9 | n | 0.000000001
- pico | 10-12 | p | 0.000000000001
- femto | 10-15 | f | 0.000000000000001
- atto | 10-18 | a | 0.000000000000000001
- zepto | 10-21 | z | 0.000000000000000000001
- yocto | 10-24 | y | 0.000000000000000000000001 base units
Common Units that Use Prefixes
- metre (length) (m)
- litre (volume) (L)
- gram (mass/weight) (g)
- joule (heat/energy) (J)
- coulomb (charge) (C)
- watt (power) (W)
- volt (electrical potential difference) (V)
- hertz (frequency) (Hz)
- newton (force) (N)
- pascal (pressure) (Pa)
- seconds (time) (s)
Other Units
These units are almost always seen in their base form, but they can use SI prefixes.
- moles (number of discreet particles in a sample) (mol)
- kelvins (temperature) (K)
- degrees Celsius (temperature) (ºC)
- amperes (electrical current) (A)
- candela (luminous intensity) (cd)
Warnings
- Remember which "direction" you are going! Check your answers against reality, if possible.⧼thumbs_response⧽
- You can only use this method if the base units are the same. Converting between kilograms and pounds, for example, requires a different formula.⧼thumbs_response⧽
References
- ↑ https://www.mathsisfun.com/definitions/kilo-.html
- ↑ https://www.nuffieldfoundation.org/sites/default/files/files/FSMA%20Convert%20lengths%20student.pdf
- ↑ https://www.rapidtables.com/convert/weight/kg-to-gram.html
- ↑ https://www.rapidtables.com/convert/power/kW_to_Watt.html
- ↑ http://physics.nist.gov/cuu/Units/prefixes.html
- ↑ https://www.montereyinstitute.org/courses/DevelopmentalMath/TEXTGROUP-1-8_RESOURCE/U06_L2_T2_text_final.html
- ↑ https://www.nist.gov/pml/weights-and-measures/metric-si-prefixes
- ↑ https://www.nist.gov/pml/weights-and-measures/metric-si-prefixes
- ↑ https://sciencenotes.org/powers-ten-metric-prefixes/



















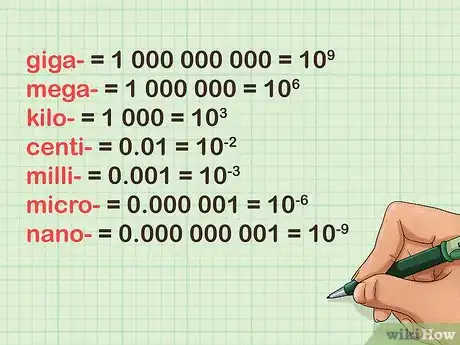


















-to-Grams-(g)-Step-8-Version-5.webp)

-to-Fahrenheit-(°F)-Step-6-Version-2.webp)












-to-Grams-(g)-Step-8-Version-5.webp)