wikiHow is a “wiki,” similar to Wikipedia, which means that many of our articles are co-written by multiple authors. To create this article, 128 people, some anonymous, worked to edit and improve it over time.
wikiHow marks an article as reader-approved once it receives enough positive feedback. This article has 81 testimonials from our readers, earning it our reader-approved status.
This article has been viewed 4,892,145 times.
Learn more...
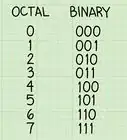
The decimal (base ten) numeral system has ten possible values (0,1,2,3,4,5,6,7,8, or 9) for each place-value. In contrast, the binary (base two) numeral system has two possible values represented as 0 or 1 for each place-value.[1] Since the binary system is the internal language of electronic computers, serious computer programmers should understand how to convert from decimal to binary.
Steps
Converter
Performing Short Division by Two with Remainder
-
1Set up the problem. For this example, let's convert the decimal number 15610 to binary. Write the decimal number as the dividend inside an upside-down "long division" symbol. Write the base of the destination system (in our case, "2" for binary) as the divisor outside the curve of the division symbol.[2]
- This method is much easier to understand when visualized on paper, and is much easier for beginners, as it relies only on division by two.
- To avoid confusion before and after conversion, write the number of the base system that you are working with as a subscript of each number. In this case, the decimal number will have a subscript of 10 and the binary equivalent will have a subscript of 2.
-
2Divide. Write the integer answer (quotient) under the long division symbol, and write the remainder (0 or 1) to the right of the dividend.[3]
- Since we are dividing by 2, when the dividend is even the binary remainder will be 0, and when the dividend is odd the binary remainder will be 1.
Advertisement -
3Continue to divide until you reach 0. Continue downwards, dividing each new quotient by two and writing the remainders to the right of each dividend. Stop when the quotient is 0.[4]
-
4Write out the new, binary number. Starting with the bottom remainder, read the sequence of remainders upwards to the top. For this example, you should have 10011100. This is the binary equivalent of the decimal number 156. Or, written with base subscripts: 15610 = 100111002[5]
- This method can be modified to convert from decimal to any base. The divisor is 2 because the desired destination is base 2 (binary). If the desired destination is a different base, replace the 2 in the method with the desired base. For example, if the desired destination is base 9, replace the 2 with 9. The final result will then be in the desired base.
Descending Powers of Two and Subtraction
-
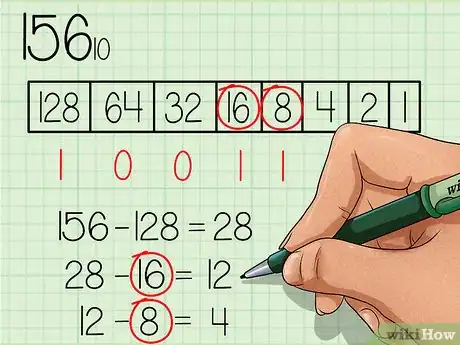
1Start by making a chart. List the powers of two in a "base 2 table" from right to left. Start at 20, evaluating it as "1". Increment the exponent by one for each power. Make the list up until you've reached a number very near the decimal system number you're starting with. For this example, let's convert the decimal number 15610 to binary.[6]
-
2Look for the greatest power of 2. Choose the biggest number that will fit into the number you are converting. 128 is the greatest power of two that will fit into 156, so write a 1 beneath this box in your chart for the leftmost binary digit. Then, subtract 128 from your initial number. You now have 28.[7]
-
3Move to the next lower power of two. Using your new number (28), move down the chart marking how many times each power of 2 can fit into your dividend. 64 does not go into 28, so write a 0 beneath that box for the next binary digit to the right. Continue until you reach a number that can go into 28.[8]
-
4Subtract each successive number that can fit, and mark it with a 1. 16 can fit into 28, so you will write a 1 beneath its box and subtract 16 from 28. You now have 12. 8 does go into 12, so write a 1 beneath 8's box and subtract it from 12. You now have 4.[9]
-
5Continue until you reach the end of your chart. Remember to mark a 1 beneath each number that does go into your new number, and a 0 beneath those that don't.[10]
-
6Write out the binary answer. The number will be exactly the same from left to right as the 1's and 0's beneath your chart. You should have 10011100. This is the binary equivalent of the decimal number 156. Or, written with base subscripts: 15610 = 100111002.[11]
- Repetition of this method will result in memorization of the powers of two, which will allow you to skip Step 1.
Community Q&A
-
QuestionHow do you convert the fractional part of a decimal to a binary?
 Community AnswerIf the decimal number has a fractional part, then the fractional parts are converted into binary by multiplying it by 2. Only the integer part of the result is noted. Repeat the multiplication until the fractional part becomes 0. Eg. 0.75 is the number we want to convert, so we'll start multiplying it by 2. 0.75 *2=1.50. Here, the fractional part is not 0 so we repeat this until the fractional part becomes 0. 1.50*2=3.00. Now take the integer part of the answer, 3, then convert it into binary. 11 is the binary form of 3. Then place the decimal point in front of the number, which is .11. Therefore, .11 is the binary form of .75
Community AnswerIf the decimal number has a fractional part, then the fractional parts are converted into binary by multiplying it by 2. Only the integer part of the result is noted. Repeat the multiplication until the fractional part becomes 0. Eg. 0.75 is the number we want to convert, so we'll start multiplying it by 2. 0.75 *2=1.50. Here, the fractional part is not 0 so we repeat this until the fractional part becomes 0. 1.50*2=3.00. Now take the integer part of the answer, 3, then convert it into binary. 11 is the binary form of 3. Then place the decimal point in front of the number, which is .11. Therefore, .11 is the binary form of .75 -
QuestionHow do I convert a mixed number to binary?
 DonaganTop AnswererConvert the mixed number to a decimal, then follow the instructions in the article above.
DonaganTop AnswererConvert the mixed number to a decimal, then follow the instructions in the article above. -
QuestionHow do I convert 0.2663 into binary?
 Jordan NewberryCommunity AnswerStart by converting 0.2663 into the fraction 2,663 / 10,000 . Use the steps above to convert 2,663 into the binary number 1010 0110 0111 and 10,000 into 10 0111 0001 0000 . So, now we have a binary fraction: 1010 0110 0111 / 10 0111 0001 0000 . Divide 1010 0110 0111 by 10 0111 0001 0000 . To do this, follow the WikiHow article: "How to Divide Binary Numbers". When you divide 1010 0110 0111 by 10 0111 0001 0000 you should get 0.0100 0100 0010... I rounded to the nearest 4,096 th.
Jordan NewberryCommunity AnswerStart by converting 0.2663 into the fraction 2,663 / 10,000 . Use the steps above to convert 2,663 into the binary number 1010 0110 0111 and 10,000 into 10 0111 0001 0000 . So, now we have a binary fraction: 1010 0110 0111 / 10 0111 0001 0000 . Divide 1010 0110 0111 by 10 0111 0001 0000 . To do this, follow the WikiHow article: "How to Divide Binary Numbers". When you divide 1010 0110 0111 by 10 0111 0001 0000 you should get 0.0100 0100 0010... I rounded to the nearest 4,096 th.
References
- ↑ http://www.binarymath.info
- ↑ https://www.youtube.com/watch?v=BFf4MYQ0iow
- ↑ http://www.inetdaemon.com/tutorials/basic_concepts/number_systems/binary/conversion.shtml
- ↑ https://www.youtube.com/watch?v=BFf4MYQ0iow
- ↑ https://www.youtube.com/watch?v=BFf4MYQ0iow
- ↑ https://x-engineer.org/undergraduate-engineering/mathematics/arithmetics/decimal-to-binary-conversion/
- ↑ https://x-engineer.org/undergraduate-engineering/mathematics/arithmetics/decimal-to-binary-conversion/
- ↑ https://x-engineer.org/undergraduate-engineering/mathematics/arithmetics/decimal-to-binary-conversion/
- ↑ https://x-engineer.org/undergraduate-engineering/mathematics/arithmetics/decimal-to-binary-conversion/
About This Article
To convert a number from decimal to binary, write down the number at the top of a sheet of paper. Divide the number by 2, and write the remainder out to the side. If you are dividing an odd number, the remainder will be 1, and if it’s even, the remainder will be 0. After you divide the number, write the result on the next line, divide it by 2, and write down the remainder. Continue this until the quotient is 0. Starting at the bottom, write down all the remainders in order. This new number is the binary conversion of the decimal. If you want to learn how to find the binary of a decimal using subtraction and the powers of 2, keep reading the article!









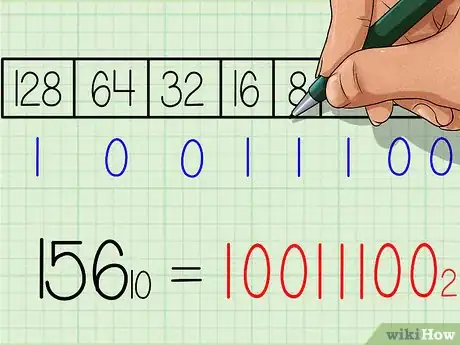



-to-Grams-(g)-Step-8-Version-5.webp)

-to-Fahrenheit-(°F)-Step-6-Version-2.webp)