How to Construct Regular Polygons Using a Circle

Last Updated: July 23, 2019 References

Constructing regular polygons accurately is very significant in geometry and is easy to do. If you have ever wondered about how to construct regular polygons from a circle, you’re reading the right article.

Method 1

Method 1 of 2:

Using A Protractor

1
Draw a straight line using the protractor. This will be the center line of your circle (dividing it into semi-circles).
2
Align the protractor so that both 0° and 180° lie on the center line. Mark the center point.

Advertisement
3
Trace the semicircle along the protractor from 0 ° to 180°.
4
Put the protractor on the other side of the center line, again with both the 0°and 180° marks on the center line.^{[1]
X
Research source}
5
Complete the circle by tracing along the protractor.
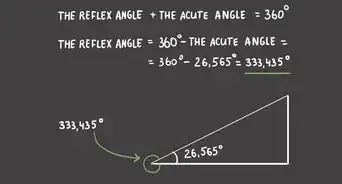
6
Calculate the angle between adjacent vertices, α. Since a circle has 360°, divide 360° by n, the number of vertices (or sides) to get α.^{[2]
X
Research source}
- α=360°/n
- α is the measured angle between lines drawn from the center of the circle to adjacent vertices.
- For a dodecagon, n=12. A dodecagon has 12 sides and 12 vertices, so 360° divided by 12 is 30°, and α=30°.
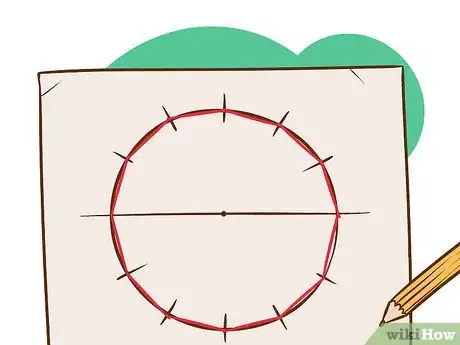
7
Mark a point for each of the successive angles. Using the protractor, mark on the circumference of the circle all the multiples of angle α calculated above.^{[3]
X
Research source}
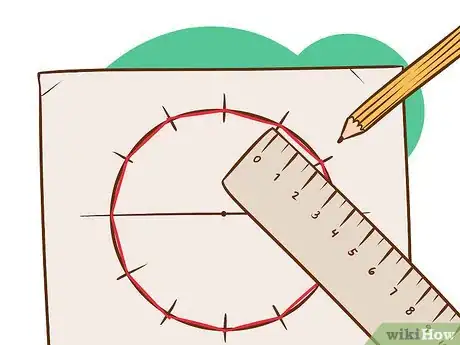
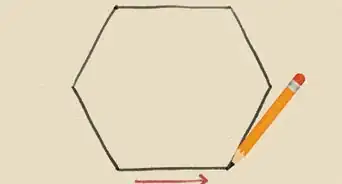
8
Join the points marked on the circle with a line segment.^{[4]
X
Research source} For a dodecagon there should be 12 marks and 12 sides, because it has 12 vertices. Don’t overlap the line segments.
- If your points are outside of the circle, then simply mark another point along the radial line from the center onto the circle for each point and then join them.
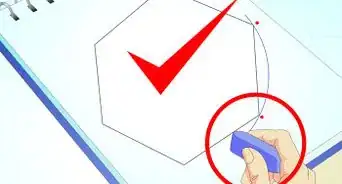
9
Check to see that the sides are the same length. If they are, you can erase the circumscribed circle.
10
Finished.

Method 2

Method 2 of 2:

Using A Compass, Ruler and Calculator

1
Draw a circle of the desired radius, r. Set your compass to the radius, r, and draw a circle.^{[5]
X
Research source}
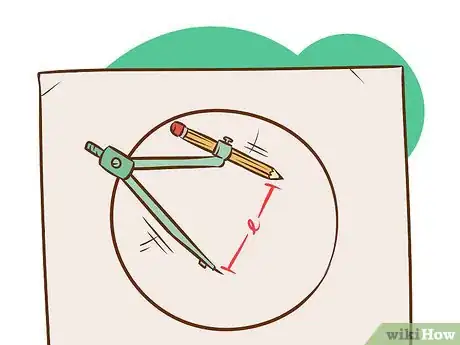
2
Calculate the length, ℓ, of each side of the regular polygon of n sides.
- ℓ=2*r*sin(180/n)^{[6]
  X
  Research source}
- 180/n is in degrees, so make sure your calculator is set for degrees, not radians.
3
Set your compass to this length, ℓ. Be ultra-accurate and triple-check the measurement to ensure that it is as accurate as possible.
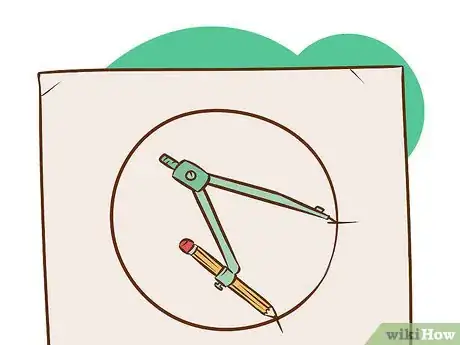
4
Start from any point on the circle and mark an arc or line. Don't change the radius of your compass.
5
Mark another arc or line on the circle. Continue the process until the arc or line touches the first point.
- Make sure your compass doesn't move!
6
Join the lines/arcs accurately using a ruler.
- Check to see that the sides are identical in length.
- If they are, then you're finished. Erase the construction guide lines.

Community Q&A

Question

How can I obtain angle 32.75 on a protractor?

Donagan

Top Answerer

With a normal protractor, all you can do is measure extremely carefully.
Question

If it is a pentagon, can I still use the compass method?

Donagan

Top Answerer

Yes.
Question

How do I construct an eleven-sided pologon

Donagan

Top Answerer

Use Method 1 above, except that the central angles used would not be 30°, they would be 360° divided by 11, or 32¾°.