How to Check if a Number Is Prime

Last Updated: September 23, 2022 References

Prime numbers are those divisible only by themselves and 1; all others are called composite numbers. While there are numerous ways to test for primality, there are trade offs. Perfect tests exist, but are extremely slow for large numbers, while much faster can give false results. Here are a few options to choose from depending on how large a number you are testing.

Part 1

Part 1 of 3:

Prime Tests

Note: In all formulas, n is the number being tested for primality.

1
Trial division test. Divide n by each prime from 2 to floor( ${\sqrt {n}}$ ).^{[1]
X
Research source}
2
Fermat's Little Theorem. Warning: false positives are possible, even for all values of a.^{[2]
X
Research source}
- Choose an integer value for a such that 2 ≤ a ≤ n - 1.
- If aⁿ (mod n) = a (mod n), then n is likely prime. If this is not true, n is not prime.
- Repeat with different values of a to increase confidence in primality
Advertisement
3
Miller-Rabin test. Warning: false positives are possible but rarely for multiple values of a.^{[3]
X
Research source}
- Find values for s and d such that $n-1=2^{s}*d$ .
- Choose an integer value for a such that 2 ≤ a ≤ n - 1.
- If a^d = +1 (mod n) or -1 (mod n), then n is probably prime. Skip to test result. Otherwise, go to next step.
- Square your answer ( $a^{2d}$ ). If this equals -1 (mod n), then n is probably prime. Skip to test result. Otherwise repeat ( $a^{4d}$ etc.) until $a^{2^{s-1}d}$ .
- If you ever square a number which is not $\pm 1$ (mod n) and end up with +1 (mod n), then n is not prime. If $a^{2^{s-1}d}\neq \pm 1$ (mod n), then n is not prime.
- Test result: If n passes test, repeat with different values of a to increase confidence.

Part 2

Part 2 of 3:

Understanding Prime Testing

1
Understand the trial division method. By the definition of primality, n is only prime if it cannot be divided evenly by integers 2 or greater.^{[4]
X
Research source} The formula given saves time by removing unnecessary tests (e.g. after testing 3 there is no need to test 9).
- Floor(x) rounds x to the closest integer ≤ x.
2
Understand modular arithmetic. The "x mod y" operation (short for "modulo") means "divide x by y and find the remainder."^{[5]
X
Research source} In other words, in modular arithmetic, numbers "wrap around" back to zero upon reaching a certain value, called the modulus. A clock counts in modulo 12: it goes from 10 to 11 to 12, then wraps around back to 1.
- Many calculators have a mod button, but see the end of this section for how to solve this by hand for large numbers.
3
Know the pitfalls of Fermat's Little Theorem. All numbers that fail this test are composite (non-prime), but unfortunately numbers that pass this test are only likely primes. If you want to be sure of avoiding false positives, look for n on a list of "Carmichael numbers" (which pass this test every time) and "Fermat pseudoprimes" (which pass this test only for some values of a).^{[6]
X
Research source}
4
Use the Miller-Rabin test whenever practical. Although tedious to perform by hand, this test is commonly used in software. This can be performed at a practical speed and gives fewer false positives than Fermat's method.^{[7]
X
Research source} A composite number never gives a false positive for more than ¼ of the values of a. If you choose several values of a at random and they all pass this test, you can be fairly confident that n is prime.^{[8]
X
Research source}
5
Perform modular arithmetic for large numbers. If you do not have access to a calculator with a mod function, or if your calculator can't display numbers that high, use properties of exponents and modular arithmetic to make the process easier.^{[9]
X
Research source} Here's an example for $3^{50}$ $3^{{50}}$ mod 50:
- Rewrite the expression with more manageable exponents: $(3^{25}*3^{25})$ mod 50. (You may need to break it down further if calculating by hand).
- $(3^{25}*3^{25})$ mod 50 = $(3^{25}$ mod 50 $*3^{25}$ mod 50) mod 50. (This is a property of modular multiplication.)
- $3^{25}$ mod 50 = 43.
- $(3^{25}$ mod 50 $*3^{25}$ mod 50) mod 50 = $(43*43)$ mod 50
- $=1849$ mod 50
- $=49$

Part 3

Part 3 of 3:

Chinese Remainder Theorem Test

1
Choose two numbers. One of the numbers is not prime and the second number is the number that needs to be tested for primality.
- "Prime1" = 35
- Prime2 = 97
2
Choose two datapoints that are greater than zero and less than prime1 and prime2 respectfully. They can't equal each other.
- Data1 = 1
- Data2 = 2
3
Calculate MMI (Mathematical Multiplicative Inverse) for Prime1 and Prime2
- Calculate MMI
  - MMI1 = Prime2 ^ -1 Mod Prime1
  - MMI2 = Prime1 ^ -1 Mod Prime2
- For Prime Numbers only (it will give a number for non-prime numbers but it won't be its MMI):
  - MMI1 = (Prime2 ^ (Prime1-2)) % Prime1
  - MMI2 = (Prime1 ^ (Prime2-2)) % Prime2
- e.g
  - MMI1 = (97 ^ 33) % 35
  - MMI2 = (35 ^ 95) % 97
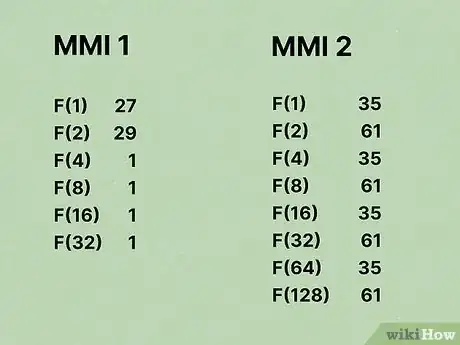
4
Create a binary table for each MMI up to Log2 of the Modulus
- For MMI1
  - F(1) = Prime2 % Prime1 = 97 % 35 = 27
  - F(2) = F(1) * F(1) % Prime1 = 27 * 27 % 35 = 29
  - F(4) = F(2) * F(2) % Prime1 = 29 * 29 % 35 = 1
  - F(8) = F(4) * F(4) % Prime1 = 1 * 1 % 35 = 1
  - F(16) =F(8) * F(8) % Prime1 = 1 * 1 % 35 = 1
  - F(32) =F(16) * F(16) % Prime1 = 1 * 1 % 35 = 1
- Calculate the binary of Prime1 - 2
  - 35 -2 = 33 (10001) base 2
  - MMI1 = F(33) = F(32) * F(1) mod 35
  - MMI1 = F(33) = 1 * 27 Mod 35
  - MMI1 = 27
- For MMI2
  - F(1) = Prime1 % Prime2 = 35 % 97 = 35
  - F(2) = F(1) * F(1) % Prime2 = 35 * 35 mod 97 = 61
  - F(4) = F(2) * F(2) % Prime2 = 61 * 61 mod 97 = 35
  - F(8) = F(4) * F(4) % Prime2 = 35 * 35 mod 97 = 61
  - F(16) = F(8) * F(8) % Prime2 = 61 * 61 mod 97 = 35
  - F(32) = F(16) * F(16) % Prime2 = 35 * 35 mod 97 = 61
  - F(64) = F(32) * F(32) % Prime2 = 61 * 61 mod 97 = 35
  - F(128) = F(64) * F(64) % Prime2 = 35 * 35 mod 97 = 61
- Calculate the binary of Prime2 - 2
  - 97 - 2 = 95 = (1011111) base 2
  - MMI2 = (((((F(64) * F(16) % 97) * F(8) % 97) * F(4) % 97) * F(2) % 97) * F(1) % 97)
  - MMI2 = (((((35 * 35) %97) * 61) % 97) * 35 % 97) * 61 % 97) * 35 % 97)
  - MMI2 = 61
5
Calculate (Data1 * Prime2 * MMI1 + Data2 * Prime1 * MMI2) % (Prime1 * Prime2)
- Answer = (1 * 97 * 27 + 2 * 35 * 61) % (97 * 35)
- Answer = (2619 + 4270) % 3395
- Answer = 99
6
Verify that "Prime1" is not Prime
- Calculate (Answer - Data1) % Prime1
- 99 -1 % 35 = 28
- Since 28 is greater than 0, 35 is not prime
7
Check if Prime2 is Prime
- Calculate (Answer - Data2) % Prime2
- 99 - 2 % 97 = 0
- Since 0 equals 0, 97 is potentially prime
8
Repeat steps 1 through 7 at least two more times.
- If step 7 is 0:
  - Use a different "prime1" where prime1 is a non-prime
  - Use a different prime 1 where prime 1 is an actual prime. In this case, steps 6 and 7 should equal 0.
  - Use different data points for data1 and data2.
- If step 7 is 0 every time, there is an extremely high probability that prime2 is prime.
- Steps 1 though 7 are known to fail in certain cases when the first number is a non-prime number and the second prime is a factor of the non-prime number "prime1". It works in all scenarios where both numbers are prime.
- The reason why steps 1 though 7 are repeated is because there are a few scenarios where, even if prime1 is not prime and prime2 is not prime, step 7 still works out to be zero, for one or both the numbers. These circumstances are rare. By changing prime1 to a different non-prime number, if prime2 is not prime, prime2 will rapidly not equal zero in step 7. Except for the instance where "prime1" is a factor of prime2, prime numbers will always equal zero in step 7.

Community Q&A

Question

Why do I use odd numbers in testing for primes?

Community Answer

Because, other than 2, there can be no even prime numbers (they would be divisible by 2).
Question

Are 57, 87, 89, and 91 prime numbers?

Gaurav Wasnik

Community Answer

57 is divisible by 3 and 19 in addition to 1 and itself so it is not prime. 87 is also divisible by 3 so it is not prime. 89 is a prime number because it is only divisible by 1 and itself. 91 is divisible by 7 so it is not prime.
Question

Is it true that since 43 x 1069 = 45,967, it can't be a prime number?

Community Answer

Yes. Prime numbers cannot be the product of any two numbers other than 1 and the number itself. So 45,967 is not prime.