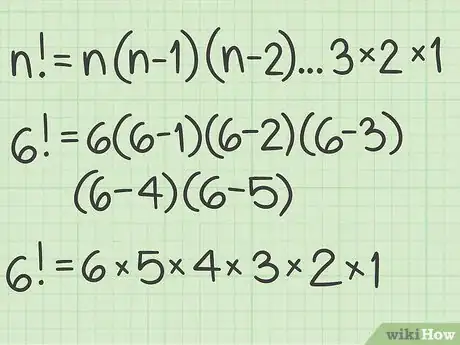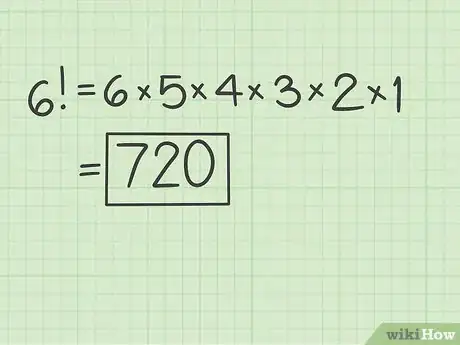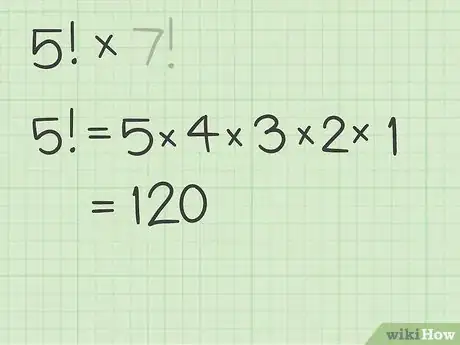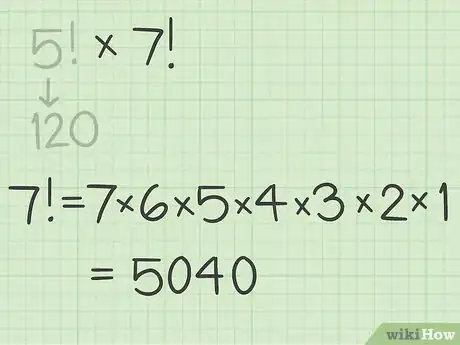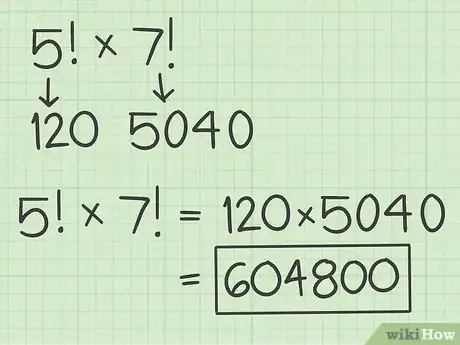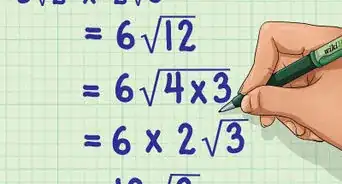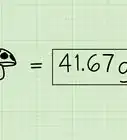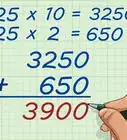This article was co-authored by wikiHow Staff. Our trained team of editors and researchers validate articles for accuracy and comprehensiveness. wikiHow's Content Management Team carefully monitors the work from our editorial staff to ensure that each article is backed by trusted research and meets our high quality standards.
There are 8 references cited in this article, which can be found at the bottom of the page.
This article has been viewed 99,540 times.
Learn more...
Factorials, denoted by a sign, are products of a whole number and all of the whole numbers below it. It is easy to calculate and multiply two factorials using a scientific calculator’s function. You can also multiply factorials by hand. The easiest way to do it is to calculate each factorial individually, and then multiply their products together. You can also use certain rules of factorials to pull out common factors, which can simplify the multiplication process.
Steps
Understanding Factorials
-
1Identify a factorial. A factorial, denoted by a whole number with an exclamation point, is the product of a series of sequential whole numbers.[1]
- For example, is a factorial.
-
2Evaluate a factorial using a formula. The formula is .[2] This means that you extend the sequence of numbers until you get to 1.
- For example,
Advertisement -
3Calculate a factorial. To calculate a factorial, begin with the denoted number, and multiply it by each sequential whole number, down to 1.[3] A quick way to calculate a factorial is to use the key on a scientific calculator. First hit the number, then hit the key to see the product.[4]
- For example, .
Calculating the Factorials Separately
-
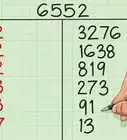
1Calculate the first factorial. Use a calculator for larger numbers. If calculating by hand, make sure you multiply each sequential number, down to 1. Rewrite the equation with this product in parentheses as the first factor.[5]
- For example, if you are calculating , first calculate :
- For example, if you are calculating , first calculate :
-
2Calculate the second factorial. You can do this by calculator or by hand, beginning on the complexity of the factorial. Rewrite the equation with this product as the second factor.[6]
- For example:
- For example:
-
3Multiply the two factorials’ products. This will give you the product of the two factorials. Since factorials tend to be large numbers, using a calculator will make this calculation easier.[7]
- For example, . So, .
Finding Common Factors
-
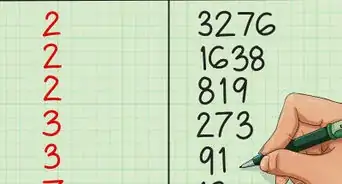
1Use a formula to factor out the largest common factorial. The formula is .[8] This means that a smaller factorial is a factor of a larger factorial.[9] For example, . When you are multiplying two factorials, the largest common factorial is the smaller of the two factorials.
- For example, if you are calculating , you can factor out from :
- For example, if you are calculating , you can factor out from :
-
2Rewrite the equation, showing the common factorial as a squared value. Then, calculate the factorial and square its product.[10]
- For example,
- For example,
-
3Multiply the remaining factors. The result will be the product of the two original factorials.[11]
- For example:
- For example:
Community Q&A
-
QuestionHow do I multiply two factorials so that the end product is also a factorial? I.e. 3! X 5!
 DonaganTop AnswererThere is no general rule covering this situation. In your example, however, (3!)(5!) = 720 = 6!.
DonaganTop AnswererThere is no general rule covering this situation. In your example, however, (3!)(5!) = 720 = 6!. -
QuestionWhat is multiplication of any number by 2 factorial?
 DonaganTop AnswererMultiplying by 2! means multiplying by 2.
DonaganTop AnswererMultiplying by 2! means multiplying by 2. -
QuestionHow do I answer this one? (k+1)! + (k+1)!
 DonaganTop AnswererMultiply (k+1)! by two.
DonaganTop AnswererMultiply (k+1)! by two.
References
- ↑ https://www.purplemath.com/modules/factorial.htm
- ↑ https://www.themathpage.com/aPreCalc/factorial.htm
- ↑ https://www.mathsisfun.com/numbers/factorial.html
- ↑ https://www.rapidtables.com/calc/math/Factorial_Calculator.html
- ↑ https://www.khanacademy.org/computing/pixar/crowds/crowds2/v/combinatorics8
- ↑ https://www.calculatorsoup.com/calculators/discretemathematics/factorials.php
- ↑ https://www.calculatorsoup.com/calculators/discretemathematics/factorials.php
- ↑ https://www.omnicalculator.com/math/factorial
- ↑ https://www.mathsisfun.com/numbers/factorial.html