How to Divide by a Two‐Digit Number

Dividing by a two-digit number is a lot like single-digit division, but it does take a little longer and some practice. Since most of us haven't memorized our 47 times tables, this can take a little guesswork, but there's a handy trick you can learn to make it faster. It also gets easier with practice, so don't get frustrated if it seems slow at first.

Part 1
Part 1 of 2:

Dividing by a Two-Digit Number

  1. Image titled Divide by a Two‐Digit Number Step 1
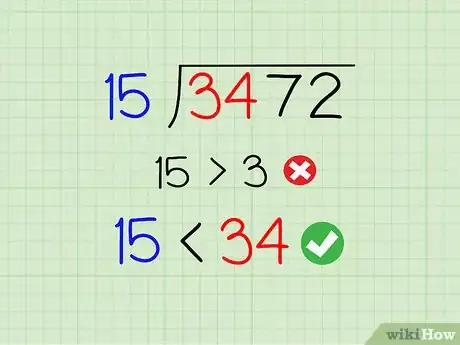
    1
    Look at the first digit of the larger number. Write the problem as a long-division problem. Just like a simpler division problem, you can start by looking at the smaller number, and asking "Does it fit into the first digit of the larger number?"[1]
    • Let's say you're solving 3472 ÷ 15. Ask "Does 15 fit into 3?" Since 15 is definitely larger than 3, the answer is "no," and we move on to the next step.
  2. Image titled Divide by a Two‐Digit Number Step 2
    2
    Look at the first two digits. Since you can't fit a two-digit number into a one-digit number, we'll look at the first two digits of the dividend instead, just like we would in a regular division problem. If you still have an impossible division problem, you'll need to look at the first three digits instead, but we don't need to in this example:[2]
    • Does 15 fit into 34? Yes, it does, so we can start calculating the answer. (The first number doesn't have to fit perfectly, it just needs to be smaller than the second number.)
    Advertisement
  3. Image titled Divide by a Two‐Digit Number Step 3
    3
    Use a little guesswork. Find out exactly how many times the first number fits into the other. You might know the answer already, but if you don't, try making a good guess and checking your answer with multiplication.[3]
    • We need to solve 34 ÷ 15, or "how many times does 15 go into 34"? You're looking for a number you can multiply with 15 to get a number less than 34, but pretty close to it:
      • Does 1 work? 15 x 1 = 15, which is less than 34, but keep guessing.
      • Does 2 work? 15 x 2 = 30. This is still less than 34, so 2 is a better answer than 1.
      • Does 3 work? 15 x 3 = 45, which is greater than 34. Too high! The answer must be 2.
  4. Image titled Divide by a Two‐Digit Number Step 4
    4
    Write the answer above the last digit you used. If you set this up like a long division problem, this should feel familiar.
    • Since you were calculating 34 ÷ 15, write the answer, 2, on the answer line above the "4."
  5. Image titled Divide by a Two‐Digit Number Step 5
    5
    Multiply your answer by the smaller number. This is the same as a normal long division problem, except we'll be using a two-digit number.[4]
    • Your answer was 2 and the smaller number in the problem is 15, so we calculate 2 x 15 = 30. Write "30" underneath the "34."
  6. Image titled Divide by a Two‐Digit Number Step 6
    6
    Subtract the two numbers. The last thing you wrote went underneath the original larger number (or part of it). Treat this as a subtraction problem and write the answer on a new line underneath.[5]
    • Solve 34 - 30 and write the answer underneath them on a new line. The answer is 4. This 4 is still "left over" after we fit 15 into 34 two times, so we'll need to use it in the next step.
  7. Image titled Divide by a Two‐Digit Number Step 7
    7
    Bring down the next digit. Just like a regular division problem, we're going to keep calculating the next digit of the answer until we've finished.[6]
    • Leave the 4 where it is and bring down the "7" from "3472" to make 47.
  8. Image titled Divide by a Two‐Digit Number Step 8
    8
    Solve the next division problem. To get the next digit, just repeat the same steps you did above for the new problem. You can use guesswork again to find the answer:[7]
    • We need to solve 47 ÷ 15:
      • 47 is bigger than our last number, so the answer will be higher. Let's try four: 15 x 4 = 60. Nope, too high!
      • We'll try three instead: 15 x 3 = 45. Smaller than 47 but close to it. Perfect.
      • The answer is 3, so we'll write that about the "7" on the answer line.
    • (If we ended up with a problem like 13 ÷ 15, with the first number smaller, we would need to bring down a third digit before we could solve it.)
  9. Image titled Divide by a Two‐Digit Number Step 9
    9
    Continue using long division. Repeat the long division steps we used before to multiply our answer by the smaller number, write the result underneath the larger number, and subtract to find the next remainder.[8]
    • Remember, we just calculated 47 ÷ 15 = 3, and now we want to find what's left over:
    • 3 x 15 = 45, so write "45" underneath the 47.
    • Solve 47 - 45 = 2. Write "2" underneath the 45.
  10. Image titled Divide by a Two‐Digit Number Step 10
    10
    Find the last digit. As before, we bring down the next digit from the original problem so we can solve the next division problem. Repeat the steps above until you find every digit in the answer.[9]
    • We've got 2 ÷ 15 as our next problem, which doesn't make much sense.
    • Bring down a digit to make 22 ÷ 15 instead.
    • 15 goes into 22 one time, so we write "1" at the end of the answer line.
    • Our answer is now 231.
  11. Image titled Divide by a Two‐Digit Number Step 11
    11
    Find the remainder. One last subtraction problem to find the final remainder, then we'll be done. In fact, if the answer to the subtraction problem is 0, you don't even need to write a remainder at all.[10]
    • 1 x 15 = 15, so write 15 underneath the 22.
    • Calculate 22 - 15 = 7.
    • We have no more digits to bring down, so instead of more division we just write "remainder 7" or "R7" at the end of our answer.
    • The final answer: 3472 ÷ 15 = 231 remainder 7
    12. Advertisement
Part 2
Part 2 of 2:

Making Good Guesses

  1. Image titled Divide by a Two‐Digit Number Step 12
    1
    Round to the nearest ten. It's not always easy to see how many times a two-digit number goes into a larger one. One useful trick is to round to the nearest multiple of 10 to make guessing easier. This comes in handy for smaller division problems, or for parts of a long division problem.
    • For example, let's say we're solving 143 ÷ 27, but we don't have a good guess at how many times 27 goes into 143. Let's pretend we're solving 143 ÷ 30 instead.
  2. Image titled Divide by a Two‐Digit Number Step 13
    2
    Count by the smaller number on your fingers. In our example, we can count by 30s instead of counting by 27s. Counting by 30 is pretty easy once you get the hang of it: 30, 60, 90, 120, 150.
    • If you find this difficult, just count by threes and add a 0 to the end.
    • Count until you get higher than the larger number in the problem (143), then stop.
  3. Image titled Divide by a Two‐Digit Number Step 14
    3
    Find the two most likely answers. We didn't hit 143 exactly, but we got two numbers close to it: 120 and 150. Let's see how many fingers we counted on to get them:
    • 30 (one finger), 60 (two fingers), 90 (three fingers), 120 (four fingers). So 30 x four = 120.
    • 150 (five fingers), so 30 x five = 150.
    • 4 and 5 are the two most likely answers to our problem.
  4. Image titled Divide by a Two‐Digit Number Step 15
    4
    Test those two numbers with the real problem. Now that we have two good guesses, let's try them out on the original problem, which was 143 ÷ 27:
    • 27 x 4 = 108
    • 27 x 5 = 135
  5. Image titled Divide by a Two‐Digit Number Step 16
    5
    Make sure you can't get any closer. Since both our numbers ended up below 143, let's try getting even closer by trying one more multiplication problem:
    • 27 x 6 = 162. This is higher than 143, so it can't be the right answer.
    • 27 x 5 came closest without going over, so 143 ÷ 27 = 5 (plus a remainder of 8, since 143 - 135 = 8.)
    6. Advertisement

Community Q&A

  • Question
    How to convert a mixed number fraction?
    Donagan
    Donagan
    Top Answerer
    To convert a mixed number to an improper fraction, multiply the denominator by the whole number, and add the original numerator. That gives you the new numerator. The denominator remains unchanged, and the whole number no longer exists.
  • Question
    How do I solve a problem that doesn't divide equally?
    Donagan
    Donagan
    Top Answerer
    Whatever is left over in the last step is shown as a "remainder" attached to the whole-number quotient.
  • Question
    I am 89 and don't know any math. Is this a problem?
    Donagan
    Donagan
    Top Answerer
    Probably not. If you've survived this long without resorting to math, there's no reason you couldn't continue to do so. Someone considerably younger than you, however, would be well advised to learn the fundamentals of math, because they can make life easier in many ways.
Advertisement

Warnings

  • If, at any point, your subtraction results in a negative number, your guess was too high. Erase that entire step and try a smaller guess.
    ⧼thumbs_response⧽
  • If, at any point, your subtraction results in a number larger than your divisor, your guess wasn't high enough. Erase that entire step and try a larger guess.
    ⧼thumbs_response⧽
Advertisement

You Might Also Like

Add and Subtract Integers
How to
Add and Subtract Integers
Calculate Percentages
How to
Calculate Percentages
Add Large Numbers
How to
Add Large Numbers
Do Long Division
How to
Do Long Division
Do Long Multiplication
How to
Do Long Multiplication
Do Division
How to
Do Division
Do Double Digit Multiplication
How to
Do Double Digit Multiplication
Cross MultiplyHow to Cross Multiply Fractions
Divide Fractions by a Whole Number
How to
Divide Fractions by a Whole Number
Multiply
How to
Multiply
Divide Mixed Fractions
How to
Divide Mixed Fractions
Divide a Whole Number by a Decimal
How to
Divide a Whole Number by a Decimal
Do Short Division
How to
Do Short Division
Divide Binary Numbers
How to
Divide Binary Numbers
Advertisement

References

  1. ↑ http://www.aaamath.com/div4db2r.htm
  2. ↑ https://www.homeschoolmath.net/teaching/md/two_digit_divisor.php
  3. ↑ https://www.mathsisfun.com/numbers/division.html
  4. ↑ https://www.mathsisfun.com/long_division.html
  5. ↑ https://sciencing.com/divide-three-digit-number-8298722.html
  6. ↑ https://www.mathsisfun.com/long_division.html
  7. ↑ https://www.cuemath.com/numbers/long-division/
  8. ↑ https://www.cuemath.com/numbers/long-division/
  9. ↑ https://www.calculatorsoup.com/calculators/math/longdivision.php
  1. ↑ https://www.mathsisfun.com/long_division2.html

About This Article

wikiHow is a “wiki,” similar to Wikipedia, which means that many of our articles are co-written by multiple authors. To create this article, 51 people, some anonymous, worked to edit and improve it over time. This article has been viewed 499,878 times.
187 votes - 55%
Co-authors: 51
Updated: January 31, 2023
Views: 499,878
Categories: Multiplication and Division
Article SummaryX

To divide by a two-digit number, try to determine whether that number would fit into the first 2 digits of the dividend. If it does, write down how many times it will go into those numbers. Follow the same rules of division that you would with a smaller number. Calculate the remainder, if any, and add the remainder as a prefix to the next number in the dividend. Continue solving the problem to either a whole number with a remainder or a decimal. For tips on estimating the answer, read on!

Did this summary help you?
Advertisement