Clear explanation of Karma-kun's answer to the final math problem in Assassination Classroom?

Question

I've been trying to understand Karma-kun's answer to the math problem in the Examination Finals.

I have searched for references and explanations for the problem but to no avail. I still couldn't understand the horrible explanations for the problem, and the answer assumes that you know their thought process is, which I don't.

This has an English translation of the problem:

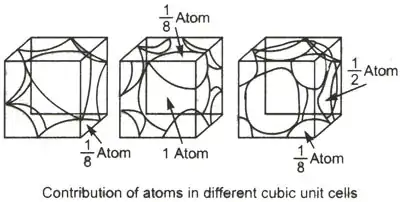
The translated problem reads: “As shown in the diagram to the right, line segment A aligns itself periodically into a cube, and atoms are located at each vertex. Within, forming a uniform crystal lattice structure, Na, K, and other alkali metals attack the crystal lattice. Within the cube, focus on a certain atom A and within the points in the nearby space, let D represent the area that comprises the atoms closest to A. Find the volume of D.”

This is a better worded question that I found on mangahere in the tsukkomis. Credits to the writer: “A bunch of atoms surround Atom A. Imaginary lines of length (a) from the centers of the atoms form a cube around A. Find the volume Atom A takes up, if it has the same volume as all the atoms. Hint: use the volume of the cube.”

Another link I found mentioned the problem but not explaining it.

There is also a YouTube video that explains Karma-kun's answer but even with his explanation, I still can't understand how he came to the conclusion that the area of the center atom is equal to half the area of the cube divided by two. a^3/2.

The reason I'm posting this is that there is no other way for me to understand the problem without asking in a thread. I just want an explanation of the answer from a "high-school" level perspective, not a professional Ph.D. level one. I don't want to hear "equidistant", "infinitesimal", "vertex" or any other technical terms that I can't comprehend.

I know I demand too much, but please help me understand how Karma-kun got a^3/2. The only perspective that I got from Karma is that all 8 atoms form a cube of their own, and the middle point of that imaginary cube is equivalent to all the atoms inside the 8 individual cubes.

And the video says so as well, but how the in the world has it gone from A 1/8 to 2A? and then a^3/2

as shown here:

For Asano-kun’s solving method, I think? https://math.stackexchange.com/questions/3193480/how-can-we-calculate-the-volume-of-a-bcc-wigner-seitz-cell-based-on-a-imaginar — Kayrab Cebll, Jul 18 '19 at 10:08

score 12 · Accepted Answer · edited Dec 21 '22 at 05:52

12

All the atoms in the crystal lattice are identical. Let's say the volume of an atom at the vertex (not corner, if it is a corner, you will need a slightly different reasoning) is B. Each atom at the vertex takes up (1/8)B of the cube. See diagram.

_{(source: sciencehq.com)}

For a cube with length a, it consists of the central atom A with volume D and 8 atoms at the vertices each taking up (1/8)B of the cube. Thus,

a³ = D + 8 × (1/8)B

However, since we know that the atoms at the vertices are actually identical to the central atom, The volume B is equal to D and hence,

a³ = B + 8 × (1/8)B ==> B = (1/2)a³

QED

All the technical terms that you have mentioned are what I was learning in my high school. This question is not hard, as Karma has said. It is a combined question of maths and chemistry.

edited Dec 21 '22 at 05:52

Glorfindel

235
1
5
12

answered Oct 18 '16 at 16:27

icefire112233

356
3
8

But why is it **over 2** in the formula a^3/2 ?? – user28781 Oct 18 '16 at 21:53
Over 2 here just tells you that, for a cube, only half of the volume will be the volume taken up by a particular atom A, the rest of the volume is to be shared by other atoms. – icefire112233 Oct 18 '16 at 22:54
So if I am following you right, **A/8 * 8 = A**, and that the eight vertices is takes up 2 atoms, meaning **2A**. then since **A** is half of the cube, then we do **A/2A**... and to calculate the volume of the atom we multiply the **x, y, z** which is **3D** and we end up with the formula to find the area of the cube **a^3** right? then we half it so **over 2?** **a^3/2** – user28781 Oct 19 '16 at 09:20
No, the eight atoms at the vertices take up space of one atom in the cube. A/2A is used to find the ratio of the volume taken up by the central atom to the total volume comprising the central atom and atoms at the vertices. So, from that we know that atom A takes up 1/2 of the volume of the cube and thus a^3/2. – icefire112233 Oct 19 '16 at 10:49
I get it now thank you for giving me a simple answer, I just had a typo there that I couldn't fix mean **A/8 * 8 = A** + _the eight vertices takes up 2 atoms_ **2A**. – user28781 Oct 19 '16 at 11:00
Every atom is equivalent - this means, every atom can be center, but also it may be vertex for closest atoms. In every cube, center atom takes some volume (let's call it C), and 8 vertexes are taking part of test volume (lets call it V). So, **A^3 = C + 8 * V**. But we can also consider center as vertex for 8 adjacent cubes. As we said before, every vertex takes 1/8 of volume, which is not occupied by center. Per each of 8 adjacent cubes. Which mean, volume of atom can be also considered as 8 small volumes. Than **8 * V = C**. That means, **A^3 = C + C** => **C = A^3 / 2**. – lentinant Oct 19 '16 at 12:19

score 4 · Answer 2 · edited Jan 19 '23 at 11:23

Here's a perhaps simpler explanation. I just got to this problem in the anime and wanted to solve it before they revealed the answer.

Ok. You have a cube with an atom in the middle. What you'll want to do is break the cube into eight pieces. Take one of these pieces. There are two atoms on opposite corners (vertexes). One of these atoms is the central atom [A]0 and the other is the atom on the edge. It goes by simple logic that exactly half of this eighth of a cube is closer to one atom than the other. This goes for all the other 8 pieces, so the volume of the cube closer to the central atom is simply half the total volume.

The problem is much simpler than it appears and I admit computing the volume by geometric pieces before I realized I was being dumb. It doesn't require very much math. Just a solid grasp of logic and a bit of cleverness.

score 2 · Answer 3 · answered Dec 19 '18 at 07:22

Supposedly, the answer itself in the manga isn't even correct. If the atoms occupy the same amount of space within each cube, then they would be one half of (a) - the invisible lines). You could essentially plug it into the formula for solving the volume of a sphere which is four over three times pi times r to the power 3. In this case, your r (radius) is a/2 (because the atoms take up the same amount of space, therefore one atom would take up one half of the invisible line)

Basically, you would do V = 4/3*π*(a/2)^3

V = 4/3*π*a^3/8

V = 4 (in 4/3) cancels out the 8 (In a^3/8) so you get 1/3*π*a^3/2

V = π*a^3/6

Misc: * = times, ^ = to the power of, π = pi.

Clear explanation of Karma-kun's answer to the final math problem in Assassination Classroom?

3 Answers3