11

When they are explaining Dimension W, it is represented as the negative side of the X axis. Why is Dimension W negative X? Is it not really it's own dimension?

Picture from Dimension W anime

giraffesyo
  • 8,519
  • 10
  • 52
  • 89
  • 5
    Presumably because the person who designed that graphic was not mathematically-inclined. – senshin Feb 26 '16 at 01:52
  • 1
    Try drawing a 4 dimensional graph on a 2 dimensional surface. This is what they came up with (your right though it is not a great graph). – NendoTaka Mar 02 '16 at 18:12

1 Answers1

2

As @NendoTaka has mentioned, it's pretty hard to draw a 4d object on a 2d surface.

Here's how dimensionality work:

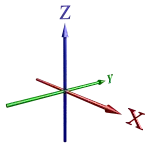
enter image description here

with a single dimension, a point is sent out infinitely, creating a line (See X)

in 2d, we add a dimension perpendicular to that (See X,Y).

Then, we go perpendicular again and expand upwards to get the third dimension(See X,Y,Z).

Because 3d > 2d, we can't represent that well on paper without folding the paper or adding more sheets on top of it - all really impractical for viewing on a screen. So, instead we use perspective - how our eyes perceive 3d. Usually the angles here are ~30 degrees.

enter image description here

And that looks pretty okay, because our eyes don't see in this traditional 3d sense, so mimicking that works. But, when we want to represent a 4th dimension, we don't have something to compare that to. We need to go perpendicular again and this is hard for our eyes to comprehend as we don't have much of a reference.

Here's an example depiction of a 4th dimension:

enter image description here

This is a more correct way to display the dimension, but it still relies on perspective - also it isn't immediately obvious that it is a new dimension on first glance.

The animators probably chose to do something simple that would be easier to animate. Although, if you rotate the above image, the X and W dimensions could overlap - and this wouldn't be obvious in the image without arrow pointers.

So yeah, they are wrong - but there's also not a simple way to represent 4 dimensions on a single sheet of paper

Coordinate Image sources & a good read

Community
  • 1
Toshinou Kyouko
  • 34,175
  • 26
  • 160
  • 297
  • 1
    To be fair, there are many standard ways of projecting 4-dimensional objects like tesseracts and 3-spheres into 3 dimensions (and then down to 2 dimensions in the usual ways) that are vastly superior to the one used in the show, many of which have the added bonus of [looking cooler than the one used in the show](http://math.stackexchange.com/q/147592/). – senshin Apr 04 '16 at 19:21
  • @senshin oh for sure, but I guess the animators also wanted to explain something, rather than astound – Toshinou Kyouko Apr 04 '16 at 19:28
  • 1
    You could use other things than position to indicate how far along an axis something is, like [color](https://en.wikipedia.org/wiki/Domain_coloring). – кяαzєя Apr 05 '16 at 00:37